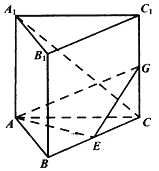
【題目】如圖，在三棱柱
中，
平面ABC，
，E是BC的中點(diǎn)，
．
求異面直線AE與
所成的角的大小；
若G為
中點(diǎn)，求二面角
的余弦值．
【答案】（1）
；（2）
【解析】
（1）以
分別為
軸建立空間直角坐標(biāo)系，利用向量
的夾角公式，求得夾角的余弦值，然后求得夾角的大小.（2）通過計(jì)算平面
和平面
的法向量，利用空間向量夾角公式，計(jì)算得二面角的余弦值.
解：
在三棱柱
中，
平面ABC，
，
E是BC的中點(diǎn)，
．
以A為原點(diǎn)，AB為x軸，AC為y軸，
為z軸，建立空間直角坐標(biāo)系，
0，
，
0，，
2，，
1，，
0，
，
1，，
2，
，
設(shè)異面直線AE與
所成的角為
，
則
，
，
異面直線AE與所成的角為．
2，
，
2，，
設(shè)平面AGE的法向量
y，
，
則
，取
，得
，
平面ACG的法向量
0，，
設(shè)二面角
的平面角為
，
．
二面角的余弦值為．
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】通過研究學(xué)生的學(xué)習(xí)行為，心理學(xué)家發(fā)現(xiàn)，學(xué)生接受能力依賴于老師引入概念和描述問題所用的時(shí)間，講座開始時(shí)，學(xué)生的興趣激增，中間有一段不太長(zhǎng)的時(shí)間，學(xué)生的興趣保持理想的狀態(tài)，隨后學(xué)生的注意力開始分散.分析結(jié)果和實(shí)驗(yàn)表明，用
表示學(xué)生掌握和接收概念的能力（的值越大，表示接受能力越強(qiáng)），
表示提出和講授概念的時(shí)間（單位：分鐘），可以有以下公式：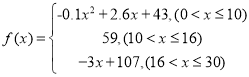
(1)開講多少分鐘后，學(xué)生的接受能力最強(qiáng)？能維持多長(zhǎng)時(shí)間？
(2)開講5分鐘與開講20分鐘比較，學(xué)生的接受能力何時(shí)強(qiáng)一些？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】為了引導(dǎo)居民合理用水，某市決定全面實(shí)施階梯水價(jià)．階梯水價(jià)原則上以住宅（一套住宅為一戶）的月用水量為基準(zhǔn)定價(jià)，具體劃分標(biāo)準(zhǔn)如表：
階梯級(jí)別 | 第一階梯水量 | 第二階梯水量 | 第三階梯水量 |
月用水量范圍（單位：立方米） |
|
|
|
從本市隨機(jī)抽取了10戶家庭，統(tǒng)計(jì)了同一月份的月用水量，得到如圖莖葉圖：
（1）現(xiàn)要在這10戶家庭中任意選取3家，求取到第二階梯水量的戶數(shù)
的分布列與數(shù)學(xué)期望；
（2）用抽到的10戶家庭作為樣本估計(jì)全市的居民用水情況，從全市依次隨機(jī)抽取10戶，若抽到
戶月用水量為二階的可能性最大，求的值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知
是橢圓
的左、右焦點(diǎn)，點(diǎn)
在橢圓
上，線段
與
軸的交點(diǎn)
滿足
.
（1）求橢圓的標(biāo)準(zhǔn)方程；
（2）過點(diǎn)
作不與
軸重合的直線
，設(shè)與圓
相交于
兩點(diǎn)，與橢圓相交于
兩點(diǎn)，當(dāng)
且
時(shí)，求
的面積
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】三角形面積為
，
，
，
為三角形三邊長(zhǎng)，
為三角形內(nèi)切圓半徑，利用類比推理，可以得出四面體的體積為（ ）
A. 
B. 
C. 
（
為四面體的高）
D. 
（其中
，
，
，
分別為四面體四個(gè)面的面積，為四面體內(nèi)切球的半徑，設(shè)四面體的內(nèi)切球的球心為
，則球心到四個(gè)面的距離都是）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】下列命題中正確的是( )
A.若a，b是兩條直線，且a∥b，那么a平行于經(jīng)過b的任何平面
B.若直線a和平面α滿足a∥α，那么a與α內(nèi)的任何直線平行
C.平行于同一條直線的兩個(gè)平面平行
D.若直線a，b和平面α滿足a∥b，a∥α，b不在平面α內(nèi)，則b∥α
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】對(duì)于函數(shù)
，若在定義域內(nèi)存在實(shí)數(shù)
，滿足
，則稱
為“
類函數(shù)”.
（1）已知函數(shù)
，試判斷
是否為“
類函數(shù)”？并說明理由；
（2）設(shè)
是定義在
上的“
類函數(shù)”，求是實(shí)數(shù)
的最小值；
（3）若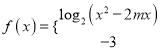
為其定義域上的“
類函數(shù)”，求實(shí)數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)
．
（1）若函數(shù)
在
上為減函數(shù)，求實(shí)數(shù)
的最小值；
（2）若存在
，使
成立，求實(shí)數(shù)
的取值范圍．
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com
