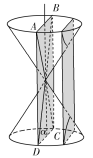
【題目】古希臘數學家阿波羅尼斯在他的著作《圓錐曲線論》中記載了用平面切割圓錐得到圓錐曲線的方法.如圖，將兩個完全相同的圓錐對頂放置(兩圓錐的軸重合)，已知兩個圓錐的底面半徑均為1，母線長均為3，記過圓錐軸的平面
為平面
(與兩個圓錐側面的交線為
)，用平行于的平面截圓錐，該平面與兩個圓錐側面的交線即雙曲線
的一部分，且雙曲線的兩條漸近線分別平行于，則雙曲線的離心率為（ ）
A.
B.
C.
D.
亮點激活精編提優100分大試卷系列答案科目：高中數學 來源： 題型：
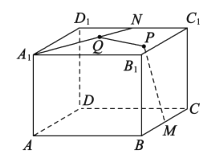
【題目】已知長方體
中，底面ABCD的長AB=4，寬BC=4，高
=3，點M，N分別是BC，
的中點，點P在上底面
中，點Q在
上，若
，則PQ長度的最小值是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝x2＋ax＋b，g(x)＝ex(cx＋d)，若曲線y＝f(x)和曲線y＝g(x)都過點P(0，2)，且在點P處有相同的切線y＝4x＋2．
(1)求a，b，c，d的值；
(2)若x≥－2時，恒有f(x)≤kg(x)，求k的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
，
是兩個不重合的平面，在下列條件中，可判斷平面，平行的是（ ）
A.
，
是平面內兩條直線，且
，
B.，是兩條異面直線，
，
，且，
C.面內不共線的三點到的距離相等
D.面，都垂直于平面
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，點
在橢圓上.
（1）求橢圓的方程；
（2）過橢圓的右焦點
作互相垂直的兩條直線
、
，其中直線交橢圓于
兩點，直線交直線
于
點，求證：直線
平分線段
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】每年的寒冷天氣都會帶熱“御寒經濟”，以餐飲業為例，當外面太冷時，不少人都會選擇叫外賣上門，外賣商家的訂單就會增加，下表是某餐飲店從外賣數據中抽取的5天的日平均氣溫與外賣訂單數.
（Ⅰ）經過數據分析，一天內平均氣溫
與該店外賣訂單數
（份）成線性相關關系，試建立關于
的回歸方程，并預測氣溫為
時該店的外賣訂單數（結果四舍五入保留整數）；
（Ⅱ）天氣預報預測未來一周內（七天），有3天日平均氣溫不高于
，若把這7天的預測數據當成真實數據，則從這7天任意選取2天，求恰有1天外賣訂單數不低于160份的概率.
附注：回歸方程
中斜率和截距的最小二乘估計公式分別為：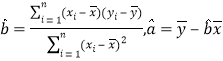
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了美化校園，要對校園內某一區域作如下設計，如圖，已知
，
，
，在邊BC上選一點P. 沿著AP和CP重新栽種花木，圖中陰影部分鋪上草坪. AP段栽種花木費用是每米3a元，CP段栽種花木費用是每米2a元，其中a是正常數.設
.
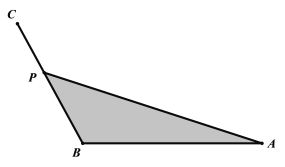
（1）求栽種花木費用y關于θ的函數表達式；
（2）求
的值，使得栽種花木費用y最小.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列
是公差為d（
）的等差數列，它的前n項和記為
，數列
是公比為q（
）的等比數列，它的前n項和記為
.若
，且存在不小于3的正整數
，使
.
（1）若
，求
.
（2）若
試比較
與
的大小，并說明理由；
（3）若
，是否存在整數m，k，使
若存在，求出m，k的值；若不存在，說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
