
【題目】已知定義在![]() 上的函數
上的函數![]() 是奇函數.
是奇函數.
(1)求![]() 的值;
的值;
(2)若對任意的![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1) a=b=1;(2) ![]() .
.
【解析】試題分析:
(1)奇函數滿足f(0)=0,據此可得b=1,結合奇函數滿足f(-x)=-f(x)可得a=1;
(2)利用題意結合函數的單調性和奇偶性得到關于實數k的不等式,求解不等式可得![]() 的取值范圍是
的取值范圍是![]() .
.
試題解析:
(1)∵f(x)是定義在R上的奇函數,
∴![]() , 解得b=1,
, 解得b=1,
∴![]() ,
,
![]()
∴a2x+1=a+2x,即a(2x﹣1)=2x﹣1對一切實數x都成立,
∴a=1, 故a=b=1. (2)∵a=b=1, ∴![]() ,
,
∴f(x)在R上是減函數.
∵不等式f(t﹣2t2)+f(﹣k)>0,
∴f(t﹣2t2)>﹣f(﹣k),
∴f(t﹣2t2)>f(k),
∵f(x)是R上的減函數, ∴t﹣2t2<k
∴![]() 對t∈R恒成立,
對t∈R恒成立,
∴![]() .
.


 文敬圖書課時先鋒系列答案
文敬圖書課時先鋒系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,已知曲線![]() 的參數方程為
的參數方程為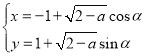 (
(![]() 為參數,
為參數,![]() ).
).
(Ⅰ)當![]() 時,若曲線
時,若曲線![]() 上存在
上存在![]() 兩點關于點
兩點關于點![]() 成中心對稱,求直線
成中心對稱,求直線![]() 的參數方程;
的參數方程;
(Ⅱ)在以原點為極點,![]() 軸正半軸為極軸的極坐標系中,極坐標方程為
軸正半軸為極軸的極坐標系中,極坐標方程為![]() 的直線
的直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,若
兩點,若![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C對應邊分別是a,b,c,c=2,sin2A+sin2B﹣sin2C=sinAsinB.
(1)若sinC+sin(B﹣A)=2sin2A,求△ABC面積;
(2)求AB邊上的中線長的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,
, ![]() )為奇函數,且相鄰兩對稱軸間的距離為
)為奇函數,且相鄰兩對稱軸間的距離為![]() .
.
(1)當![]() 時,求
時,求![]() 的單調遞減區間;
的單調遞減區間;
(2)將函數![]() 的圖象沿
的圖象沿![]() 軸方向向右平移
軸方向向右平移![]() 個單位長度,再把橫坐標縮短到原來的
個單位長度,再把橫坐標縮短到原來的![]() (縱坐標不變),得到函數
(縱坐標不變),得到函數![]() 的圖象.當
的圖象.當![]() 時,求函數
時,求函數![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}的前n項和為Sn , 且Sn=2n﹣1.數列{bn}滿足b1=2,bn+1﹣2bn=8an .
(1)求數列{an}的通項公式.
(2)證明:數列{ ![]() }為等差數列,并求{bn}的通項公式.
}為等差數列,并求{bn}的通項公式.
(3)求{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為了解2017屆高三學生的性別和喜愛游泳是否有關,對100名高三學生進行了問卷調查,得到如下列聯表:
喜歡游泳 | 不喜歡游泳 | 合計 | |
男生 | 10 | ||
女生 | 20 | ||
合計 |
已知在這100人中隨機抽取1人,抽到喜歡游泳的學生的概率為![]() .
.
(Ⅰ)請將上述列聯表補充完整;
(Ⅱ)判斷是否有99.9%的把握認為喜歡游泳與性別有關?
附: 
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家父母記錄了女兒玥玥的年齡(歲)和身高(單位cm)的數據如下:
年齡x | 6 | 7 | 8 | 9 |
身高y | 118 | 126 | 136 | 144 |
(1)試求y關于x的線性回歸方程 ![]() =
= ![]() x+
x+ ![]()
(2)試預測玥玥10歲時的身高.(其中, ![]() =
= 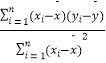 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在棱長為2的正方體![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別是棱
分別是棱![]() ,
, ![]() ,
, ![]() ,
, ![]() 的中點,點
的中點,點![]() ,
, ![]() 分別在棱
分別在棱![]() ,
, ![]() 上移動,且
上移動,且![]() .
.
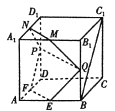
(1)當![]() 時,證明:直線
時,證明:直線![]() 平面
平面![]() ;
;
(2)是否存在![]() ,使面
,使面![]() 與面
與面![]() 所成的二面角為直二面角?若存在,求出
所成的二面角為直二面角?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】山西某公司有一批專業技術人員,對他們進行年齡狀況和接受教育程度(本科學歷)的調查,其結果(人數分布)如表:
學歷 | 35歲以下 | 35 | 50歲以上 |
本科 | 80 | 30 | 20 |
研究生 |
| 20 |
|
(Ⅰ)用分層抽樣的方法在![]() 歲年齡段的專業技術人員中抽取一個容量為10的樣本,將該樣本看成一個總體,從中任取3人,求至少有1人的學歷為研究生的概率;
歲年齡段的專業技術人員中抽取一個容量為10的樣本,將該樣本看成一個總體,從中任取3人,求至少有1人的學歷為研究生的概率;
(Ⅱ)在這個公司的專業技術人員中按年齡狀況用分層抽樣的方法抽取![]() 個人,其中35歲以下48人,50歲以上10人,再從這
個人,其中35歲以下48人,50歲以上10人,再從這![]() 個人中隨機抽取出1人,此人的年齡為50歲以上的概率為
個人中隨機抽取出1人,此人的年齡為50歲以上的概率為![]() ,求
,求![]() 、
、![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com