
【題目】設(shè)函數(shù)![]()
(1) 判斷并證明f(x)在定義域內(nèi)的單調(diào)性;
(2)證明:當(dāng)x>-1時, ![]() ;
;
(3)設(shè)當(dāng)x≥0時, ![]() ,求a的取值范圍.
,求a的取值范圍.
【答案】(1)增;(2)見解析; (3) ![]() .
.
【解析】試題分析:(1) 求出![]() ,
, ![]() 得增區(qū)間,
得增區(qū)間, ![]() 得減區(qū)間;(2)將函數(shù)
得減區(qū)間;(2)將函數(shù)![]() 的解析式代入
的解析式代入![]() 整理成
整理成![]() ,組成新函數(shù)
,組成新函數(shù)![]() ,然后根據(jù)其導(dǎo)函數(shù)判斷單調(diào)性進而可求函數(shù)
,然后根據(jù)其導(dǎo)函數(shù)判斷單調(diào)性進而可求函數(shù)![]() 的最小值
的最小值![]() ,進而
,進而![]() 可得證;(3)先確定函數(shù)
可得證;(3)先確定函數(shù)![]() 的取值范圍,然后對
的取值范圍,然后對![]() 分
分![]() 和
和![]() 兩種情況進行討論,當(dāng)
兩種情況進行討論,當(dāng)![]() 時根據(jù)
時根據(jù)![]() 的范圍可直接得到
的范圍可直接得到![]() 不成立;當(dāng)
不成立;當(dāng)![]() 時,令
時,令![]() ,然后對函數(shù)
,然后對函數(shù)![]() 進行求導(dǎo),根據(jù)導(dǎo)函數(shù)判斷單調(diào)性并求出最值,求
進行求導(dǎo),根據(jù)導(dǎo)函數(shù)判斷單調(diào)性并求出最值,求![]() 的范圍.
的范圍.
試題解析:(1) 在定義域![]() 內(nèi)增
內(nèi)增
(2)當(dāng)![]() 時,
時, ![]() 當(dāng)且僅當(dāng)
當(dāng)且僅當(dāng)![]() .
.
令![]() ,則
,則![]() .
.
當(dāng)![]() 時
時![]() ,g(x)在
,g(x)在![]() 是減函數(shù);當(dāng)
是減函數(shù);當(dāng)![]() 時
時![]() ,g(x)在
,g(x)在![]() 是增函數(shù).
是增函數(shù).
于是函數(shù)g(x)在![]() 處達到最小值,因而當(dāng)
處達到最小值,因而當(dāng)![]() 時,
時, ![]() ,即
,即![]() .
.
所以當(dāng)![]() 時,
時, ![]() .
.
(3)由題意![]() ,此時
,此時![]() ,
,
當(dāng)![]() 時,若
時,若![]() ,則
,則![]() ,
, ![]() 不成立;
不成立;
當(dāng)![]() 時,令
時,令![]() ,則
,則![]() 當(dāng)且僅當(dāng)
當(dāng)且僅當(dāng)![]() .
.
![]() .
.
由(1)知![]() ,即
,即![]() ,
,
![]() .
.
(ⅰ)當(dāng)![]() 時,
時, ![]() ,h(x)在
,h(x)在![]() 是減函數(shù),
是減函數(shù), ![]() ,即
,即![]() .
.
(ⅱ)當(dāng)![]() 時,由(ⅰ)知
時,由(ⅰ)知![]() ,即
,即![]() ,
,
![]() ,
,
當(dāng)![]() 時,
時, ![]() ,所以
,所以![]() ,即
,即![]() .
.
綜上,a的取值范圍是![]() .
.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】寧夏某市2008年至2012年新建商品住宅每平方米的均價![]() (單位:千元)的數(shù)據(jù)如下表:
(單位:千元)的數(shù)據(jù)如下表:
年份 | 2008 | 2009 | 2010 | 2011 | 2012 |
年份序號x | 1 | 2 | 3 | 4 | 5 |
每平米均價y | 2.0 | 3.1 | 4.5 | 6.5 | 7.9 |
(Ⅰ)求y關(guān)于x的線性回歸方程![]() ;
;
(Ⅱ)利用(Ⅰ)中的回歸方程,分析從2008年到2012年該市新建商品住宅每平方米均價的變化情況,并預(yù)測該市2015年新建商品住宅每平方米的均價.
附:回歸直線的斜率和截距的最小二乘估計公式分別為
 ,
, ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】有2名老師,3名男生,3名女生站成一排照相留念,在下列情況中,各有多少種不同站法?
(1)3名男生必須站在一起;
(2)2名老師不能相鄰;
(3)若3名女生身高都不等,從左到右女生必須由高到矮的順序站.(最終結(jié)果用數(shù)字表示)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知雙曲線![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
, ![]() 為坐標(biāo)原點,
為坐標(biāo)原點, ![]() 是雙曲線上在第一象限內(nèi)的點,直線
是雙曲線上在第一象限內(nèi)的點,直線![]() 分別交雙曲線
分別交雙曲線![]() 左、右支于另一點
左、右支于另一點![]() ,
, ![]() ,且
,且![]() ,則雙曲線
,則雙曲線![]() 的離心率為( )
的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
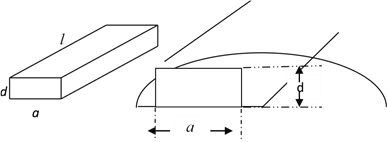
【題目】一根水平放置的長方體形枕木的安全負荷與它的寬度![]() 成正比,與它的厚度
成正比,與它的厚度![]() 的平方成正比,與它的長度
的平方成正比,與它的長度![]() 的平方成反比.
的平方成反比.
(Ⅰ)將此枕木翻轉(zhuǎn)90°(即寬度變?yōu)楹穸龋砟镜陌踩摵蓵绾巫兓繛槭裁矗浚ㄔO(shè)翻轉(zhuǎn)前后枕木的安全負荷分別為![]() 且翻轉(zhuǎn)前后的比例系數(shù)相同都為
且翻轉(zhuǎn)前后的比例系數(shù)相同都為![]() )
)
(Ⅱ)現(xiàn)有一根橫斷面為半圓(已知半圓的半徑為![]() )的木材,用它來截取成長方體形的枕木,其長度為10,問截取枕木的厚度為
)的木材,用它來截取成長方體形的枕木,其長度為10,問截取枕木的厚度為![]() 多少時,可使安全負荷
多少時,可使安全負荷![]() 最大?
最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
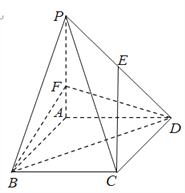
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是菱形,
是菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上的一個動點,
上的一個動點, ![]() 為
為![]() 的中點.
的中點.
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求證:
,求證: ![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,其中
,其中![]() .
.
(1)若函數(shù)![]() 為偶函數(shù),求實數(shù)
為偶函數(shù),求實數(shù)![]() 的值;
的值;
(2)求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值;
上的最大值;
(3)若方程![]() 有且僅有一個解,求實數(shù)
有且僅有一個解,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,函數(shù)
,函數(shù)![]() .
.
(1)若函數(shù)![]() ,
, ![]() 的最小值為-16,求實數(shù)
的最小值為-16,求實數(shù)![]() 的值;
的值;
(2)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上是單調(diào)減函數(shù),求實數(shù)
上是單調(diào)減函數(shù),求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)當(dāng)![]() 時,不等式
時,不等式![]() 的解集為
的解集為![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某知名品牌汽車深受消費者喜愛,但價格昂貴。某汽車經(jīng)銷商退出![]() 三種分期付款方式銷售該品牌汽車,并對近期100位采用上述分期付款的客戶進行統(tǒng)計分析,得到如下的柱狀圖。已知從
三種分期付款方式銷售該品牌汽車,并對近期100位采用上述分期付款的客戶進行統(tǒng)計分析,得到如下的柱狀圖。已知從![]() 三種分期付款銷售中,該經(jīng)銷商每銷售此品牌汽車1輛所獲得的利潤分別是1萬元,2萬元,3萬元。現(xiàn)甲乙兩人從該汽車經(jīng)銷商處,采用上述分期付款方式各購買此品牌汽車一輛。以這100 位客戶所采用的分期付款方式的頻率代替1位客戶采用相應(yīng)分期付款方式的概率。
三種分期付款銷售中,該經(jīng)銷商每銷售此品牌汽車1輛所獲得的利潤分別是1萬元,2萬元,3萬元。現(xiàn)甲乙兩人從該汽車經(jīng)銷商處,采用上述分期付款方式各購買此品牌汽車一輛。以這100 位客戶所采用的分期付款方式的頻率代替1位客戶采用相應(yīng)分期付款方式的概率。
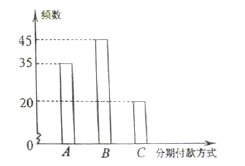
(Ⅰ)求甲乙兩人采用不同分期付款方式的概率;
(Ⅱ)記![]() (單位:萬元)為該汽車經(jīng)銷商從甲乙兩人購車中所獲得的利潤,求
(單位:萬元)為該汽車經(jīng)銷商從甲乙兩人購車中所獲得的利潤,求![]() 的分布列和期望。
的分布列和期望。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com