
【題目】已知![]() 是數列
是數列![]() 的前n項和,
的前n項和,![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)對于正整數![]() ,已知
,已知![]() 成等差數列,求正整數
成等差數列,求正整數![]() 的值;
的值;
(3)設數列![]() 前n項和是
前n項和是![]() ,且滿足:對任意的正整數n,都有等式
,且滿足:對任意的正整數n,都有等式![]() 成立.求滿足等式
成立.求滿足等式![]() 的所有正整數n.
的所有正整數n.
【答案】(1)![]() (2)
(2)![]() (3)1和3.
(3)1和3.
【解析】試題分析:(1)先根據和項與通項關系得項之間遞推關系,再根據等比數列定義判斷,最后根據等比數列通項公式求結果,(2)根據等差數列化簡得![]() ,再根據正整數限制條件以及指數性質確定不定方程正整數解,(3)先根據定義求數列
,再根據正整數限制條件以及指數性質確定不定方程正整數解,(3)先根據定義求數列![]() 通項公式,再根據等差數列求和公式求
通項公式,再根據等差數列求和公式求![]() ,根據數列相鄰項關系確定
,根據數列相鄰項關系確定![]() 遞減,最后根據單調性求正整數解.
遞減,最后根據單調性求正整數解.
試題解析:(1)由![]()
![]() 得
得![]() ,兩式作差得
,兩式作差得![]() ,即
,即![]()
![]() .
.
![]() ,
,![]() ,所以
,所以![]()
![]() ,
,![]() ,則
,則![]()
![]() ,所以數列
,所以數列![]() 是首項為
是首項為![]() 公比為
公比為![]() 的等比數列,所以
的等比數列,所以![]()
![]() ;
;
(2)由題意![]() ,即
,即![]() ,
,
所以![]() ,其中
,其中![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
![]() ,所以
,所以![]() ,
,![]() ,
,![]() ;
;
(3)由![]()
![]()
![]() 得,
得,
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]() ,
,
所以![]()
![]() ,即
,即![]() ,
,
所以![]()
![]() ,
,
又因為![]() ,得
,得![]() ,所以
,所以![]()
![]() ,
,
從而![]()
![]()
![]() ,
,![]() ,
,
當![]() 時
時![]() ;當
;當![]() 時
時![]() ;當
;當![]() 時
時![]() ;
;
下面證明:對任意正整數![]() 都有
都有![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
當![]() 時,
時,![]()
![]() ,即
,即![]() ,
,
所以當![]() 時,
時,![]() 遞減,所以對任意正整數
遞減,所以對任意正整數![]() 都有
都有![]() ;
;
綜上可得,滿足等式![]() 的正整數
的正整數![]() 的值為
的值為![]() 和
和![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中數學 來源: 題型:
【題目】E為正四面體D﹣ABC棱AD的中點,平面α過點A,且α∥平面ECB,α∩平面ABC=m,α∩平面ACD=n,則m、n所成角的余弦值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知 ![]() 在橢圓C:
在橢圓C: ![]() 上,F為右焦點,PF⊥垂直于x軸,A,B,C,D為橢圓上的四個動點,且AC,BD交于原點O.
上,F為右焦點,PF⊥垂直于x軸,A,B,C,D為橢圓上的四個動點,且AC,BD交于原點O.
(1)求橢圓C的方程;
(2)判斷直線l: ![]() 與橢圓的位置關系;
與橢圓的位置關系;
(3)設A(x1 , y1),B(x2 , y2)滿足 ![]() =
= ![]() ,判斷kAB+kBC的值是否為定值,若是,請求出此定值,并求出四邊形ABCD面積的最大值,否則說明理由.
,判斷kAB+kBC的值是否為定值,若是,請求出此定值,并求出四邊形ABCD面積的最大值,否則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校10位同學組成的志愿者組織分別由李老師和楊老師負責.每次獻愛心活動均需該組織4位同學參加.假設李老師和楊老師分別將各自活動通知的信息獨立、隨機地發給4位同學,且所發信息都能收到.則甲同學收到李老師或楊老師所發活動通知信息的概率為
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在高為2的梯形ABCD中,AB∥CD,AB=2,CD=5,過A、B分別作AE⊥CD,BF⊥CD,垂足分別為E、F.已知DE=1,將梯形ABCD沿AE、BF同側折起,得空間幾何體ADE﹣BCF,如圖2. 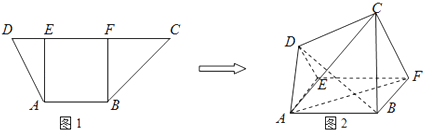
(Ⅰ)若AF⊥BD,證明:△BDE為直角三角形;
(Ⅱ)若DE∥CF, ![]() ,求平面ADC與平面ABFE所成角的余弦值.
,求平面ADC與平面ABFE所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓的兩個焦點為F1(﹣ ![]() ,0),F2(
,0),F2( ![]() ,0),M是橢圓上一點,若
,0),M是橢圓上一點,若 ![]()
![]() =0,|
=0,| ![]() ||
|| ![]() |=8.
|=8.
(1)求橢圓的方程;
(2)點P是橢圓上任意一點,A1、A2分別是橢圓的左、右頂點,直線PA1 , PA2與直線x= ![]() 分別交于E,F兩點,試證:以EF為直徑的圓交x軸于定點,并求該定點的坐標.
分別交于E,F兩點,試證:以EF為直徑的圓交x軸于定點,并求該定點的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com