【題目】(本題滿分14分)
已知正項數(shù)列
滿足：對任意正整數(shù)
，都有
成等差數(shù)列，
成等比數(shù)列，且
（Ⅰ）求證：數(shù)列
是等差數(shù)列；
（Ⅱ）求數(shù)列的通項公式；
(Ⅲ) 設
如果對任意正整數(shù)，不等式
恒成立，求實數(shù)
的取值范圍．
【答案】（Ⅰ）詳見解析；（Ⅱ）詳見解析；（Ⅲ）
【解析】分析：(I)通過已知得到關(guān)于數(shù)列的項的兩個等式,處理方程組得到
,利用等差數(shù)列的定義得證；〔II〕利用等差數(shù)列的通項公式求出
，求出
；（III） 先通過裂項求和的方法求出
，代入
化簡得到關(guān)于
的二次不等式恒成立，構(gòu)造新函數(shù)，通過對二次項系數(shù)的討論求出函數(shù)的最大值，令最大值小于
，求出
的范圍.
詳解：（I）由已知，得
①，
② .
由②得
③.將③代入①得，
對任意
，有
即
是等差數(shù)列.
（Ⅱ）設數(shù)列
的公差為
，
由
經(jīng)計算，得
（Ⅲ）由（1）得
不等式
化為
即
設
，則
對任意正整數(shù)
恒成立．
當
，即
時，不滿足條件；
當
，即
時，滿足條件；
當
，即
時，
的對稱軸為
，關(guān)于遞減，
因此，只需
解得
綜上，
100分闖關(guān)期末沖刺系列答案
名校聯(lián)盟快樂課堂系列答案科目：高中數(shù)學 來源： 題型：
【題目】2002年國際數(shù)學家大會在北京召開，會標是以我國古代數(shù)學家趙爽的弦圖為基礎設計.弦圖是由四個全等的直角三角形與一個小正方形拼成的一個大正方形(如圖)如果小正方形的邊長為1，大正方形的邊長為5，直角三角形中較小的銳角為
，則
( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在直角坐標系xoy中，其中A(0,0),B(2,0),C(1,1),D(0,1),圖中圓弧所在圓的圓心為點C，半徑為 
，且點P在圖中陰影部分（包括邊界）運動.若 
，其中 
，則 
的取值范圍是（ ）
A.[2,3+ 
]
B.[2,3+ 
]
C.[3- 
, 3+ ]
D.[3- 
, 3+ ]
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知數(shù)列{an}滿足：a1=1，|an+1－an|=pn，n∈N*，Sn為數(shù)列{an}的前n項和.
（1）若{an}是遞增數(shù)列，且a1，2a2，3a3成等差數(shù)列，求p的值；
（2）若p=
，且{a2n－1}是遞增數(shù)列，{a2n}是遞減數(shù)列，求數(shù)列{an}的通項公式；
（3）在（2）的條件下，令cn=n（an+1－an），求數(shù)列{cn}的前n項和Tn.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知矩形ABCD中，E、F分別是AB、CD上的點，BE=CF=1，BC=2，AB=CD=3，P、Q分別為DE、CF的中點，現(xiàn)沿著EF翻折，使得二面角A﹣EF﹣B大小為 
．
（Ⅰ）求證：PQ∥平面BCD；
（Ⅱ）求二面角A﹣DB﹣E的余弦值．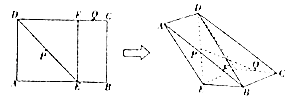
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】過 
軸上動點 
引拋物線 
的兩條切線 
、 
， 
、 
為切點，設切線 、 的斜率分別為 
和 
.
（Ⅰ）求證： 
；
（Ⅱ）求證：直線 
恒過定點，并求出此定點坐標；
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知△ABC的面積為3，且滿足0≤
≤6，設
與
的夾角為θ.
(1)求θ的取值范圍；
(2)求函數(shù)f(θ)＝2sin2
－
(cos θ＋sin θ)·(cos θ－sin θ)的最大值與最小值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知定義在
上的奇函數(shù)
滿足
,且在
上是增函數(shù);
定義行列式
; 函數(shù)
(其中
)．
(1) 證明: 函數(shù)在
上也是增函數(shù);
(2) 若函數(shù)
的最大值為4，求
的值;
(3) 若記集合M={m|恒有g(
)<0},
,求
．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
