
已知函數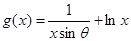 在
在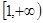 上為增函數,
上為增函數,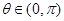 ,
,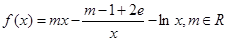
(1)求 的值;
的值;
(2)當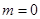 時,求函數
時,求函數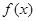 的單調區間和極值;
的單調區間和極值;
(3)若在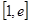 上至少存在一個
上至少存在一個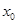 ,使得
,使得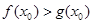 成立,求
成立,求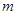 的取值范圍.
的取值范圍.
(1) 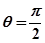 ;
;
(2) 函數的單調增區間是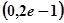 ,遞減區間為
,遞減區間為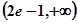 ,
, 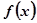 有極大值為
有極大值為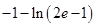 ;
;
(3) 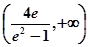 .
.
解析試題分析:(1)因為函數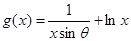 在
在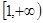 上為增函數,所以
上為增函數,所以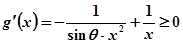 在
在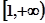 上恒成立;由此可有
上恒成立;由此可有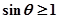 ,由
,由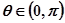 知
知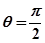 .
.
(2) 令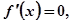 則
則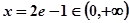 ,根據
,根據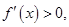 函數單調遞增,
函數單調遞增,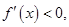 函數單調遞減,即函數的單調增區間是
函數單調遞減,即函數的單調增區間是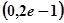 ,遞減區間為
,遞減區間為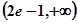 ,
,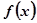 有極大值為
有極大值為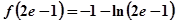 .
.
(3) 令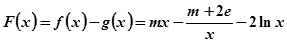 ,分情況討論:
,分情況討論:
?當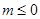 時,
時,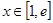 有
有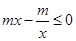 ,
,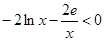 ,所以:
,所以: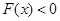
即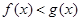 在
在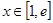 恒成立,此時不存在
恒成立,此時不存在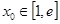 使得
使得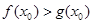 成立
成立
?當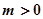 時,
時,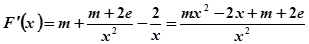
∵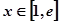 ,∴
,∴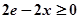 , 又
, 又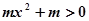 ,∴
,∴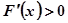 在
在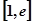 上恒成立。
上恒成立。
∴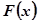 在
在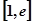 上單調遞增,∴
上單調遞增,∴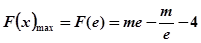
令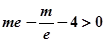 ,則
,則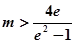 故所求
故所求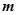 的取值范圍為
的取值范圍為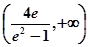
(1)由已知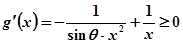 在
在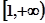 上恒成立
上恒成立
即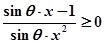 ∵
∵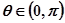 ,∴
,∴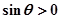
故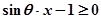 在
在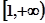 上恒成立,只需
上恒成立,只需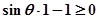
即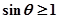 ,∴只有
,∴只有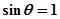 ,由
,由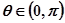 知
知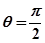 3分
3分
(2)∵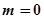 ,∴
,∴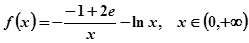 ,
,
∴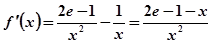 (4分),
(4分),
令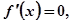 則
則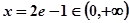
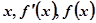 的變化情況如下表:
的變化情況如下表: