【題目】在極坐標系中，曲線C的極坐標方程為
.以極點為原點，極軸為x軸的正半軸建立平面直角坐標系，直線l的參數方程為
(t為參數)
(1)若
，求曲線C的直角坐標方程以及直線l的極坐標方程；
(2)設點
，曲線C與直線
交于A、B兩點，求
的最小值
科目：高中數學 來源： 題型：
【題目】某市正在進行創建全國文明城市的復驗工作，為了解市民對“創建全國文明城市”的知識知曉程度，某權威調查機構對市民進行隨機調查，并對調查結果進行統計，共分為優秀和一般兩類，先從結果中隨機抽取100份，統計得出如下
列聯表：
優秀 | 一般 | 總計 | |
男 | 25 | 25 | 50 |
女 | 30 | 20 | 50 |
總計 | 55 | 45 | 100 |
（1）根據上述列聯表，是否有
的把握認為“創城知識的知曉程度是否為優秀與性別有關”？
（2）現從調查結果為一般的市民中，按分層抽樣的方法從中抽取9人，然后再從這9人中隨機抽取3人，求這三位市民中男女都有的概率；
（3）以樣本估計總體，視樣本頻率為概率，從全市市民中隨機抽取10人，用
表示這10人中優秀的人數，求隨機變量的期望和方差.
附：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
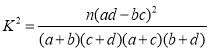（其中
）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設矩陣M＝
(其中a>0，b>0)．
(1)若a＝2，b＝3，求矩陣M的逆矩陣M－1；
(2)若曲線C：x2＋y2＝1在矩陣M所對應的線性變換作用下得到曲線C′：
＋y2＝1，求a，b的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某調查機構對全國互聯網行業進行調查統計，得到整個互聯網行業從業者年齡分布餅狀圖，90后從事互聯網行業崗位分布條形圖，則下列結論中不正確的是（ ）
注：90后指1990年及以后出生，80后指1980-1989年之間出生，80前指1979年及以前出生.
A.互聯網行業從業人員中90后占一半以上
B.互聯網行業中從事技術崗位的人數超過總人數的
C.互聯網行業中從事運營崗位的人數90后比80前多
D.互聯網行業中從事技術崗位的人數90后比80后多
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，已知拋物線C：
（
）的焦點F在直線
上，平行于x軸的兩條直線
，
分別交拋物線C于A，B兩點，交該拋物線的準線于D，E兩點.
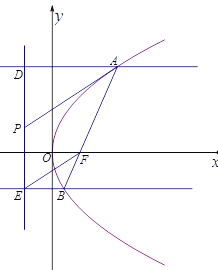
（1）求拋物線C的方程；
（2）若F在線段
上，P是
的中點，證明：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左焦點坐標為
，
，
分別是橢圓的左，右頂點，
是橢圓上異于，的一點，且
，
所在直線斜率之積為
.
（1）求橢圓
的方程；
（2）過點
作兩條直線，分別交橢圓于
，
兩點（異于
點）.當直線
，
的斜率之和為定值
時，直線
是否恒過定點？若是，求出定點坐標；若不是，請說明理.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在“互聯網+”時代的今天，移動互聯快速發展，智能手機（Smartphone）技術不斷成熟，尤其在5G領域，華為更以
件專利數排名世界第一，打破了以往由美、英、日壟斷的前三位置，再次榮耀世界，而華為的價格卻不斷下降，遠低于蘋果；智能手機成為了生活中必不可少的工具，學生是對新事物和新潮流反應最快的一個群體之一，越來越多的學生在學校里使用手機，為了解手機在學生中的使用情況，對某學校高二年級
名同學使用手機的情況進行調查，針對調查中獲得的“每天平均使用手機進行娛樂活動的時間”進行分組整理得到如下的數據：
使用時間（小時） | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
所占比例 | 4% | 10% | 31% | 16% |
| 12% | 2% |
（1）求表中
的值；
（2）從該學校隨機選取一名同學，能否根據題目中所給信息估計出這名學生每天平均使用手機進行娛樂活動小于
小時的概率？若能，請算出這個概率；若不能，請說明理由；
（3）若從使用手機
小時和
小時的兩組中任取兩人，調查問卷，看看他們對使用手機進行娛樂活動的看法，求這
人都使用小時的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】手工藝是一種生活態度和對傳統的堅持，在我國有很多手工藝品制作村落，村民的手工技藝世代相傳，有些村落制造出的手工藝品不僅全國聞名，還大量遠銷海外.近年來某手工藝品村制作的手工藝品在國外備受歡迎，該村村民成立了手工藝品外銷合作社，為嚴把質量關，合作社對村民制作的每件手工藝品都請3位行家進行質量把關，質量把關程序如下：（i）若一件手工藝品3位行家都認為質量過關，則該手工藝品質量為A級；（ii）若僅有1位行家認為質量不過關，再由另外2位行家進行第二次質量把關，若第二次質量把關這2位行家都認為質量過關，則該手工藝品質量為B級，若第二次質量把關這2位行家中有1位或2位認為質量不過關，則該手工藝品質量為C級；（iii）若有2位或3位行家認為質量不過關，則該手工藝品質量為D級.已知每一次質量把關中一件手工藝品被1位行家認為質量不過關的概率為
，且各手工藝品質量是否過關相互獨立.
（1）求一件手工藝品質量為B級的概率；
（2）若一件手工藝品質量為A，B，C級均可外銷，且利潤分別為900元，600元，300元，質量為D級不能外銷，利潤記為100元.
①求10件手工藝品中不能外銷的手工藝品最有可能是多少件；
②記1件手工藝品的利潤為X元，求X的分布列與期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
