
��֪���タ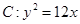 ���c(di��n)
���c(di��n)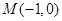 ���^
���^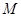 ��ֱ��
��ֱ�� �����タ
�����タ ��
�� ���c(di��n).
���c(di��n).
��1��������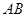 ���c(di��n)�ęM����(bi��o)����
���c(di��n)�ęM����(bi��o)����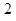 ����ֱ��
����ֱ�� ��б�ʣ�
��б�ʣ�
��2���O(sh��)�c(di��n)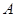 �P(gu��n)��
�P(gu��n)�� �S��(du��)�Q�c(di��n)��
�S�Č�(du��)�Q�c(di��n)��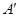 �����C��ֱ��
�����C��ֱ��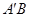 �^���c(di��n).
�^���c(di��n).
��1��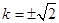 ;��2��
;��2��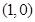
����ԇ�}��������1����?y��n)��c(di��n)M�ڒ��タ���棬�����^M�c���タ�ཻ��ֱ��б�ʴ��ڣ����c(di��n)бʽ���O(sh��)ֱ�����̲�(li��n)�����タ���̣���ȥy�����ɵ�һ��(g��)�P(gu��n)��x��һԪ���η��̣����f�_(d��)��������֪���c(di��n)�ęM����(bi��o)���������б�ʵ�ֵ.
��2�����c(di��n)A,B�ęM����(bi��o)�M�㣨1��ʽ�е�һԪ���η��̣����f�_(d��)�����ɵø��cϵ��(sh��)�ĵ�ʽ���ٌ���ֱ��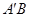 �ķ��̣������c(di��n)����c(di��n)A,B������(bi��o)���뒁�タ����.�������ֱ���^���c(di��n)��Ҫ���c(di��n)�Ƿ���ڵ��ж�.
�ķ��̣������c(di��n)����c(di��n)A,B������(bi��o)���뒁�タ����.�������ֱ���^���c(di��n)��Ҫ���c(di��n)�Ƿ���ڵ��ж�.
ԇ�}��������1���O(sh��)�^�c(di��n)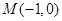 ��ֱ�����̞�
��ֱ�����̞�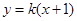 ��
��
�� 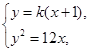 ��
��
��?y��n)? ����
����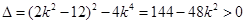 ��
��
���ԣ�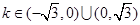 .
.
�O(sh��)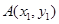 ��
�� ���t
���t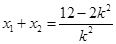 ��
��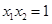 .
.
��?y��n)龀��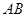 ���c(di��n)�ęM����(bi��o)����
���c(di��n)�ęM����(bi��o)����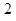 ������
������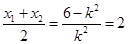 ��
��
���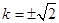 �������}��.
�������}��.
��2�����}��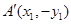 ��ֱ��
��ֱ��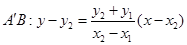 ��
��
�� 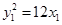 ��
�� ��
��
���� 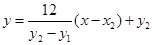
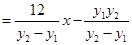
��?y��n)? �� ��
�� ��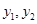 ̖ͬ(h��o)������
̖ͬ(h��o)������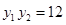 ��
��
���� 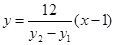 ��
��
���ԣ�ֱ��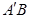 ���^���c(di��n)
���^���c(di��n)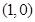 .
.
���c(di��n)��1.ֱ���c���タ��λ���P(gu��n)ϵ.2.�ⷽ�̵�����.3.���^���c(di��n)�Ć��}.4.ֱ�����̵ı�ʾ.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��D���E�A ���x���ʞ�
���x���ʞ� ��
�� �S������
�S������ �صõľ����L����
�صõľ����L���� �Ķ��S�L��
�Ķ��S�L�� �c
�c �S�Ľ��c(di��n)��
�S�Ľ��c(di��n)�� ���^����(bi��o)ԭ�c(di��n)
���^����(bi��o)ԭ�c(di��n) ��ֱ��
��ֱ�� �c
�c �ཻ���c(di��n)
�ཻ���c(di��n) ��ֱ��
��ֱ��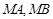 �քe�c
�քe�c �ཻ���c(di��n)
�ཻ���c(di��n) ��
��
��1���� ��
�� �ķ��̣�
�ķ��̣�
��2�����C�� ��
��
��3��ӛ ����e�քe��
����e�քe�� ����
���� ����
���� ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�p����x2-y2=2��ֱ��n��б�ʞ�2 ��ֱ��n�c�p�����ཻ��A��B���c(di��n)������AB�����c(di��n)��P��
(1)���c(di��n)P������(bi��o)��x,y)�M��ķ��̣���Ҫ��׃����ȡֵ��������
(2)�^�p���������c(di��n)F1�����Aб�Ǟ� ��ֱ��m���p������M��N���c(di��n)������
��ֱ��m���p������M��N���c(di��n)������ ��F(xi��n)2���p�������ҽ��c(di��n)�����F2MN����eS�P(gu��n)�ڃAб��
��F(xi��n)2���p�������ҽ��c(di��n)�����F2MN����eS�P(gu��n)�ڃAб�� �ı��_(d��)ʽ��
�ı��_(d��)ʽ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��ƽ��ֱ������(bi��o)ϵ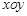 �У���(d��ng)�c(di��n)
�У���(d��ng)�c(di��n)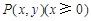 �M�㣺�c(di��n)
�M�㣺�c(di��n)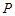 �����c(di��n)
�����c(di��n)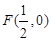 �c��
�c��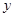 �S�ľ��x֮���
�S�ľ��x֮���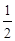 .ӛ��(d��ng)�c(di��n)
.ӛ��(d��ng)�c(di��n)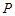 ��܉�E������
��܉�E������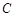 .
.
��1��������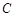 ��܉�E���̣�
��܉�E���̣�
��2���^�c(di��n)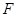 ��ֱ��������
��ֱ��������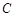 ��
�� ��
��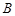 ���c(di��n)���^�c(di��n)
���c(di��n)���^�c(di��n) ��ԭ�c(di��n)
��ԭ�c(di��n)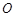 ��ֱ����ֱ��
��ֱ����ֱ��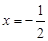 ���c(di��n)
���c(di��n)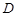 �����C��ֱ��
�����C��ֱ��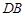 ƽ����
ƽ����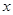 �S.
�S.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��ֱ֪��l��y��x��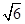 ���AO��x2��y2��5���E�AE��
���AO��x2��y2��5���E�AE��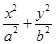 ��1(a��b��0)���x����e��
��1(a��b��0)���x����e��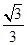 ��ֱ��l���AO�صõ����L�c�E�A�Ķ��S�L��ȣ�
��ֱ��l���AO�صõ����L�c�E�A�Ķ��S�L��ȣ�
(1)��E�AE�ķ��̣�
(2)�^�AO������һ�c(di��n)P���E�AE�ăɗl�о������о�������б�ʣ����C�����о���б��֮�e�鶨ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪���タ����c(di��n)������(bi��o)ԭ�c(di��n)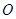 �����c(di��n)
�����c(di��n)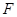 ��
��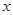 �S�ϣ����タ�ϵ��c(di��n)
�S�ϣ����タ�ϵ��c(di��n)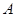 ��
��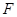 �ľ��x��2����
�ľ��x��2����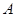 �ęM����(bi��o)��1��ֱ��
�ęM����(bi��o)��1��ֱ��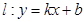 �c���タ����
�c���タ���� ��
�� ���c(di��n).
���c(di��n).
��1�����タ�ķ��̣�
��2����(d��ng)ֱ��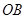 ��
��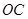 �ăAб��֮�͞�
�ăAб��֮�͞� �r(sh��)���C��ֱ��
�r(sh��)���C��ֱ��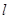 �^���c(di��n).
�^���c(di��n).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪������ԭ�c(di��n)�����c(di��n)������(bi��o)�S�ϵ��p���� ��(j��ng)�^
��(j��ng)�^ ��
�� ���c(di��n)
���c(di��n)
��1�����p���� �ķ��̣�
�ķ��̣�
��2���O(sh��)ֱ�� ���p����
���p���� ��
�� ��
�� ���c(di��n)���Ҿ���
���c(di��n)���Ҿ��� ���A
���A ��
�� ���ȷ֣���(sh��)��(sh��)
���ȷ֣���(sh��)��(sh��) ��
�� ��ֵ
��ֵ
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
���タ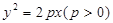 �����(zh��n)�����̞�
�����(zh��n)�����̞�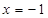 ���^��(zh��n)���c
���^��(zh��n)���c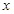 �S�Ľ��c(di��n)
�S�Ľ��c(di��n)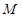 ��ֱ��
��ֱ��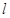 �����タ��
�����タ��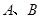 ���c(di��n).
���c(di��n).
��1�����c(di��n)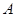 ��
��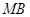 ���c(di��n)����ֱ��
���c(di��n)����ֱ��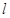 �ķ��̣�
�ķ��̣�
��2���O(sh��)���タ�Ľ��c(di��n)��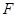 ����(d��ng)
����(d��ng)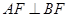 �r(sh��)����
�r(sh��)����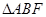 ����e��
����e��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�����}
��֪�E�A ��a>b>0�����x���ʞ�
��a>b>0�����x���ʞ� ���ҽ��c(di��n)�飨
���ҽ��c(di��n)�飨 ��0����
��0����
��I����E�A�ķ��̣�
�����^�E�A���ҽ��c(di��n)��б�ʞ�k��ֱ���c�E�A�����c(di��n)A��xl��y1��,B��x2��y2������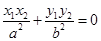 �� ��б��k�ǵ�ֵ��
�� ��б��k�ǵ�ֵ��
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com