
【題目】已知![]() ,函數
,函數![]() .
.
(1)當![]() 時,寫出
時,寫出![]() 的單調遞增區間(不需寫出推證過程);
的單調遞增區間(不需寫出推證過程);
(2)當![]() 時,若直線
時,若直線![]() 與函數
與函數![]() 的圖象相交于
的圖象相交于![]() 兩點,記
兩點,記![]() ,求
,求![]() 的最大值;
的最大值;
(3)若關于![]() 的方程
的方程![]() 在區間
在區間![]() 上有兩個不同的實數根,求實數
上有兩個不同的實數根,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)4;(3)
;(2)4;(3)![]()
【解析】
(1)當![]() 時,
時,![]() ,由此能求出
,由此能求出![]() 的單調遞增區間;
的單調遞增區間;
(2)由![]() ,得當
,得當![]() 時,
時,![]() 的圖象與直線
的圖象與直線![]() 沒有交點;當
沒有交點;當![]()
![]() 或
或![]() 時,y=f(x)
時,y=f(x)![]() 的圖象與直線
的圖象與直線![]() 只有一個交點;當
只有一個交點;當![]() 時,
時,![]() ;當
;當![]() 時,由
時,由![]() ,得
,得![]() ,由
,由![]() ,得
,得![]() ,由此能求出
,由此能求出![]() 的最大值;
的最大值;
(3)要使關于x的方程![]() 有兩個不同的實數根
有兩個不同的實數根![]() ,則
,則![]() ,且
,且![]() ,根據
,根據![]() ,且
,且![]() 進行分類討論能求出
進行分類討論能求出![]() 的取值范圍.
的取值范圍.
(1)當![]() 時,
時,![]()
在![]() 和
和![]() 單調遞增
單調遞增
(2)因為x>0,所以
(ⅰ)當a>4時,![]() ,函數的
,函數的![]() ,
,
![]() 函數的圖像與直線y=4沒有交點;
函數的圖像與直線y=4沒有交點;
(ⅱ)當a=4時,![]() ,函數的最小值是4,
,函數的最小值是4,
![]() 的圖象與直線
的圖象與直線![]() 只有一個交點;
只有一個交點;
當![]() 時,
時,![]()
![]() 與
與![]() 有1個交點,交點坐標
有1個交點,交點坐標![]() ,不滿足條件;
,不滿足條件;
(ⅲ)當0<a<4時,![]()
即![]()
![]()
![]() ,
,
![]() ,
,
![]() ;
;
(ⅳ)當a<0時,如圖:
由![]()
![]()
得![]() ,
,
解得![]() ;
;
由![]() ,
,![]()
得![]()
解得![]() .
.
所以![]() .
.
綜上:![]() 的最大值是4.
的最大值是4.
(Ⅲ)要使關于![]() 的方程
的方程![]() (*)
(*)
當![]() 時,去絕對值得
時,去絕對值得![]() ,解得
,解得![]() ,不成立,舍;
,不成立,舍;
當![]() 時,去絕對值
時,去絕對值![]() ,
,![]()
化簡為:![]() ,
,![]() 不成立,舍;
不成立,舍;
當![]() 時,
時,![]() ,
,![]() ,也不成立,舍;
,也不成立,舍;
![]()
![]() .
.
(ⅰ)當![]() 時,由(*)得
時,由(*)得![]() ,
,
所以![]() ,不符合題意;
,不符合題意;
(ⅱ)當![]() 時,由(*)得
時,由(*)得![]() ,其對稱軸
,其對稱軸![]() ,不符合題意;
,不符合題意;
(ⅲ)當![]() ,且
,且![]() 時,
時,
當![]() 時,
時,![]() ,
,![]() ,
,
整理為:![]() ,
,![]() 不成立,
不成立,
當![]() 時,
時,
要使直線![]() 與函數
與函數![]() 圖像在
圖像在![]() 內有兩個交點,
內有兩個交點,
當![]() 時,
時,![]() ,當
,當![]() 時,
時,
只需滿足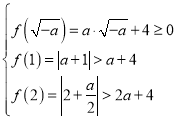
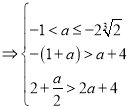 ,
,
解得:![]() ;①
;①
當![]() 時
時
![]() ,
,
整理得:![]() ,
,
若在區間![]() 方程有2個不等實數根,只需滿足
方程有2個不等實數根,只需滿足
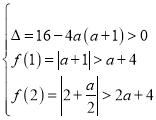
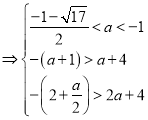 ,
,
解得:![]() ②,
②,
綜上①②可知,![]() 的范圍是
的范圍是![]()
綜上所述,a的取值范圍為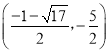 .
.


科目:高中數學 來源: 題型:
【題目】下列結論中正確的個數是( )
①正三棱錐的頂點在底面的射影到底面各頂點的距離相等;
②有兩個側面是矩形的棱柱是直棱柱;
③兩個底畫平行且相似的多面體是棱臺;
④底面是正三角形,其余各面都是等腰三角形的三棱錐一定是正三棱錐.
A.0B.1C.5D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個結論:
①當a為任意實數時,直線(a﹣1)x﹣y+2a+1=0恒過定點P,則過點P且焦點在y軸上的拋物線的標準方程是![]() ;
;
②已知雙曲線的右焦點為(5,0),一條漸近線方程為2x﹣y=0,則雙曲線的標準方程是![]() ;
;
③拋物線![]() 的準線方程為
的準線方程為![]() .
.
④已知雙曲線![]() ,其離心率e∈(1,2),則m的取值范圍是(﹣12,0).
,其離心率e∈(1,2),則m的取值范圍是(﹣12,0).
其中正確命題的序號是___________.(把你認為正確命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產一種產品,根據經驗,其次品率![]() 與日產量
與日產量![]() (萬件)之間滿足關系,
(萬件)之間滿足關系, (其中
(其中![]() 為常數,且
為常數,且![]() ,已知每生產1萬件合格的產品以盈利2萬元,但每生產1萬件次品將虧損1萬元(注:次品率=次品數/生產量, 如
,已知每生產1萬件合格的產品以盈利2萬元,但每生產1萬件次品將虧損1萬元(注:次品率=次品數/生產量, 如![]() 表示每生產10件產品,有1件次品,其余為合格品).
表示每生產10件產品,有1件次品,其余為合格品).
(1)試將生產這種產品每天的盈利額![]() (萬元)表示為日產量
(萬元)表示為日產量![]() (萬件)的函數;
(萬件)的函數;
(2)當日產量為多少時,可獲得最大利潤?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線的頂點為坐標原點,焦點![]() 在
在![]() 軸的正半軸上,點
軸的正半軸上,點![]() 是拋物線上的一點,以
是拋物線上的一點,以![]() 為圓心,2為半徑的圓與
為圓心,2為半徑的圓與![]() 軸相切,切點為
軸相切,切點為![]() .
.
(I)求拋物線的標準方程:
(Ⅱ)設直線![]() 在
在![]() 軸上的截距為6,且與拋物線交于
軸上的截距為6,且與拋物線交于![]() ,
,![]() 兩點,連接
兩點,連接![]() 并延長交拋物線的準線于點
并延長交拋物線的準線于點![]() ,當直線
,當直線![]() 恰與拋物線相切時,求直線
恰與拋物線相切時,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com