
在平面直角坐標系xOy中,直線l與拋物線y2=4x相交于不同的A、B兩點.
(1)如果直線l過拋物線的焦點,求 ·
· 的值;
的值;
(2)如果 ·
· =-4,證明直線l必過一定點,并求出該定點.
=-4,證明直線l必過一定點,并求出該定點.
(1)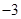 ;(2)過定點
;(2)過定點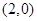 。
。
【解析】
試題分析:拋物線的焦點在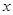 軸上,直線
軸上,直線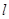 過焦點且與拋物線相交,這條直線可能與
過焦點且與拋物線相交,這條直線可能與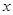 垂直,但不可能與
垂直,但不可能與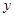 垂直,因此這種直線方程可設為
垂直,因此這種直線方程可設為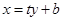 的形式,可避免討論斜率存在不存在的問題。直線與拋物線相交于兩點
的形式,可避免討論斜率存在不存在的問題。直線與拋物線相交于兩點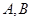 ,我們一般設
,我們一般設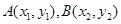 ,則
,則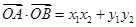 ,而這里的
,而這里的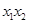 ,
,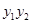 可以讓直線方程和拋物線方程聯立方程組得出。(1)中直線
可以讓直線方程和拋物線方程聯立方程組得出。(1)中直線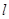 方程可設為
方程可設為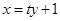 ,(2)中直線
,(2)中直線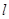 方程可設為
方程可設為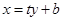 ,(2)與(1)的區別在于最后令
,(2)與(1)的區別在于最后令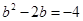 ,求出
,求出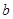 。
。
試題解析:(1)由題意:拋物線焦點為 ,
,
設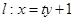 ,代入拋物線方程
,代入拋物線方程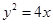 中得,
中得,
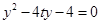 ,
,
設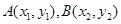 ,則
,則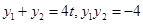 ,
,
∴
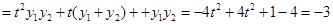 。
。
(2)設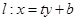 ,代入拋物線方程
,代入拋物線方程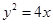 中得,
中得,
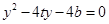 ,
,
設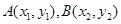 ,則
,則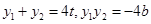 ,
,
∴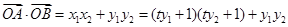
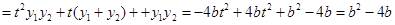 ,
,
令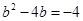 ,∴
,∴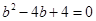 ,
,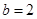 ,
,
∴直線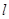 過定點
過定點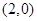 ,∴若
,∴若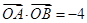 ,則直線
,則直線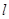 必過一定點。
必過一定點。
考點:直線與拋物線相交問題,與向量的數量積。


科目:高中數學 來源: 題型:
| 2 |
| x2 |
| a2 |
| y2 |
| 9 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在平面直角坐標系xOy中,銳角α和鈍角β的終邊分別與單位圓交于A,B兩點.若點A的橫坐標是
如圖,在平面直角坐標系xOy中,銳角α和鈍角β的終邊分別與單位圓交于A,B兩點.若點A的橫坐標是| 3 |
| 5 |
| 12 |
| 13 |
| 16 |
| 65 |
| 16 |
| 65 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 | t |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 16 |
| 7 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com