【題目】已知函數
．
（1）當
時，求曲線
在點
處的切線方程；
（2）當
時，若曲線在直線
的上方，求實數
的取值范圍．
導學全程練創優訓練系列答案科目：高中數學 來源： 題型：
【題目】隨著資本市場的強勢進入，互聯網共享單車“忽如一夜春風來”，遍布了各級城市的大街小巷，為了解我市的市民對共享單車的滿意度，某調查機構借助網絡進行了問卷調查，并從參與調查的網友中隨機抽取了50人進行分析．若得分低于60分，說明不滿意，若得分不低于60分，說明滿意，調查滿意度得分情況結果用莖葉圖表示如圖1．
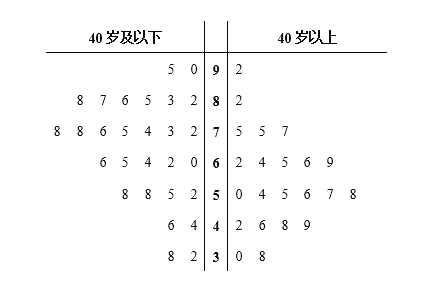
（Ⅰ）根據莖葉圖找出40歲以上網友中滿意度得分的眾數和中位數；
（Ⅱ）根據莖葉圖完成下面列聯表，并根據以上數據，判斷是否有
的把握認為滿意度與年齡有關；
滿意 | 不滿意 | 合計 | |
40歲以下 | |||
40歲以上 | |||
合計 |
（Ⅲ）先采用分層抽樣的方法從40歲及以下的網友中選取7人，再從這7人中隨機選出2人，將頻率視為概率，求選出的2人中至少有1人是不滿意的概率．
參考格式：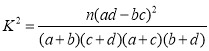
，其中
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在各項均為正數的等比數列{an}中，
，且a4+a5=6a3．
（Ⅰ）求數列{an}的通項公式；
（Ⅱ）設數列{log2an}的前n項和為Sn，求Sn的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某幼兒園雛鷹班的生活老師統計2018年上半年每個月的20日的晝夜溫差
，
和患感冒的小朋友人數（
/人）的數據如下：
溫差 |
|
|
|
|
|
|
患感冒人數 | 8 | 11 | 14 | 20 | 23 | 26 |
其中
，
，
.
（Ⅰ）請用相關系數加以說明是否可用線性回歸模型擬合與
（Ⅱ）建立關于
的回歸方程（精確到
），預測當晝夜溫差升高
時患感冒的小朋友的人數會有什么變化？（人數精確到整數）
參考數據：
．參考公式：相關系數：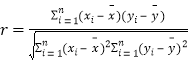
，回歸直線方程是
，
,
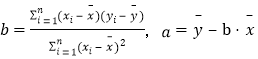查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學有學生500人，學校為了解學生的課外閱讀時間，從中隨機抽取了50名學生，獲得了他們某一個月課外閱讀時間的數據（單位：小時），將數據分為5組：[10，12），[12，14），[14，16），[16，18），[18，20]，整理得到如圖所示的頻率分布直方圖．
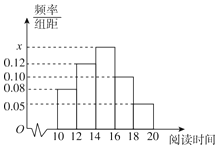
（1）求頻率分布直方圖中的x的值；
（2）試估計該校所有學生中，課外閱讀時間不小于16小時的學生人數；
（3）已知課外閱讀時間在[10，12）的樣本學生中有3名女生，現從閱讀時間在[10，12）的樣本學生中隨機抽取3人，記X為抽到女生的人數，求X的分布列與數學期望E（X）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對給定的d∈N*，記由數列構成的集合
．
（1）若數列{an}∈Ω（2），寫出a3的所有可能取值；
（2）對于集合Ω（d），若d≥2．求證：存在整數k，使得對Ω（d）中的任意數列{an}，整數k不是數列{an}中的項；
（3）已知數列{an}，{bn}∈Ω（d），記{an}，{bn}的前n項和分別為An，Bn．若|an+1|≤|bn+1|，求證：An≤Bn．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，某種螺帽是由一個半徑為2的半球體挖去一個正三棱錐構成的幾何體，該正三棱錐的底面三角形內接于半球底面大圓，頂點在半球面上，則被挖去的正三棱錐體積為_______．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
已知函數
在區間
，
內各有一個極值點．
（I）求
的最大值；
（II）當
時，設函數
在點
處的切線為
，若在點
處穿過函數的圖象（即動點在點附近沿曲線運動，經過點時，從的一側進入另一側），求函數
的表達式．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
