
【題目】已知橢圓![]() :
:![]() 的左、右有頂點(diǎn)分別是
的左、右有頂點(diǎn)分別是![]() 、
、![]() ,上頂點(diǎn)是
,上頂點(diǎn)是![]() ,圓
,圓![]() :
:![]() 的圓心
的圓心![]() 到直線
到直線![]() 的距離是
的距離是![]() ,且橢圓的右焦點(diǎn)與拋物線
,且橢圓的右焦點(diǎn)與拋物線![]() 的焦點(diǎn)重合.
的焦點(diǎn)重合.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)平行于![]() 軸的動(dòng)直線與橢圓和圓在第一象限內(nèi)的交點(diǎn)分別為
軸的動(dòng)直線與橢圓和圓在第一象限內(nèi)的交點(diǎn)分別為![]() 、
、![]() ,直線
,直線![]() 、
、![]() 與
與![]() 軸的交點(diǎn)記為
軸的交點(diǎn)記為![]() ,
,![]() .試判斷
.試判斷![]() 是否為定值,若是,證明你的結(jié)論.若不是,舉反例說(shuō)明.
是否為定值,若是,證明你的結(jié)論.若不是,舉反例說(shuō)明.

| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形, ![]() , 平面
, 平面![]() 底面
底面![]() ,且
,且![]() 是邊長(zhǎng)為
是邊長(zhǎng)為![]() 的等邊三角形,
的等邊三角形, ![]() ,
, ![]() 是
是![]() 中點(diǎn).
中點(diǎn).
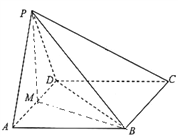
(1)求證:平面![]() 平面
平面![]() ;
;
(2)證明: ![]() , 且
, 且![]() 與
與![]() 的面積相等.
的面積相等.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知數(shù)列![]() ,
, ![]() ,
, ![]() ,
, ![]() 滿足
滿足![]() ,且當(dāng)
,且當(dāng)![]() 時(shí),
時(shí), ![]() ,令
,令![]() .
.
(Ⅰ)寫(xiě)出![]() 的所有可能的值.
的所有可能的值.
(Ⅱ)求![]() 的最大值.
的最大值.
(Ⅲ)是否存在數(shù)列![]() ,使得
,使得![]() ?若存在,求出數(shù)列
?若存在,求出數(shù)列![]() ;若不存在,說(shuō)明理由.
;若不存在,說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 在
在![]() 處的切線斜率為2.
處的切線斜率為2.
(Ⅰ)求![]() 的單調(diào)區(qū)間和極值;
的單調(diào)區(qū)間和極值;
(Ⅱ)若![]() 在
在![]() 上無(wú)解,求
上無(wú)解,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() .
.
(Ⅰ)當(dāng)![]() 在
在![]() 處切線的斜率為
處切線的斜率為![]() ,求
,求![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的前提下,求![]() 的極值;
的極值;
(Ⅲ)若![]() 有
有![]() 個(gè)不同零點(diǎn),求
個(gè)不同零點(diǎn),求![]() 的取值范圍..
的取值范圍..
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,以
中,以![]() 為極點(diǎn),
為極點(diǎn),![]() 軸非負(fù)半軸為極軸建立坐標(biāo)系,已知曲線
軸非負(fù)半軸為極軸建立坐標(biāo)系,已知曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,直線
,直線![]() 的參數(shù)方程為:
的參數(shù)方程為: 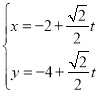 (
(![]() 為參數(shù)),兩曲線相交于
為參數(shù)),兩曲線相交于![]() 兩點(diǎn).
兩點(diǎn).
(1)寫(xiě)出曲線![]() 的直角坐標(biāo)方程和直線
的直角坐標(biāo)方程和直線![]() 的普通方程;
的普通方程;
(2)若![]() 求
求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某班為了活躍元旦晚會(huì)氣氛,主持人請(qǐng)12位同學(xué)做一個(gè)游戲,第一輪游戲中,主持人將標(biāo)有數(shù)字1到12的十二張相同的卡片放入一個(gè)不透明的盒子中,每人依次從中取出一張卡片,取到標(biāo)有數(shù)字7到12的卡片的同學(xué)留下,其余的淘汰;第二輪將標(biāo)有數(shù)字1到6的六張相同的卡片放入一個(gè)不透明的盒子中,每人依次從中取出一張卡片,取到標(biāo)有數(shù)字4到6的卡片的同學(xué)留下,其余的淘汰;第三輪將標(biāo)有數(shù)字1,2,3的三張相同的卡片放入一個(gè)不透明的盒子中,每人依次從中取出一張卡片,取到標(biāo)有數(shù)字2,3的卡片的同學(xué)留下,其余的淘汰;第四輪用同樣的辦法淘汰一位同學(xué),最后留下的這位同學(xué)獲得一個(gè)獎(jiǎng)品.已知同學(xué)甲參加了該游戲.
(1)求甲獲得獎(jiǎng)品的概率;
(2)設(shè)![]() 為甲參加游戲的輪數(shù),求
為甲參加游戲的輪數(shù),求![]() 的分布列與數(shù)學(xué)期望.
的分布列與數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】“干支紀(jì)年法”是中國(guó)歷法上自古以來(lái)使用的紀(jì)年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被稱為“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”。“天干”以“甲”字開(kāi)始,“地支”以“子”字開(kāi)始,兩者按干支順序相配,組成了干支紀(jì)年法,其相配順序?yàn)椋杭鬃印⒁页蟆⒈镉希仔纭⒁液ァ⒈印锬咨辍⒁矣稀⒈纭锼龋驳玫?/span>![]() 個(gè)組成,周而復(fù)始,循環(huán)記錄。2014年是“干支紀(jì)年法”中的甲午年,那么2020年是“干支紀(jì)年法”中的()
個(gè)組成,周而復(fù)始,循環(huán)記錄。2014年是“干支紀(jì)年法”中的甲午年,那么2020年是“干支紀(jì)年法”中的()
A. 己亥年 B. 戊戌年 C. 庚子年 D. 辛丑年
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,點(diǎn)
中,點(diǎn)![]() ,直線
,直線![]() ,設(shè)圓
,設(shè)圓![]() 的半徑為1, 圓心在
的半徑為1, 圓心在![]() 上.
上.

(1)若圓心![]() 也在直線
也在直線![]() 上,過(guò)點(diǎn)
上,過(guò)點(diǎn)![]() 作圓
作圓![]() 的切線,求切線方程;
的切線,求切線方程;
(2)若圓![]() 上存在點(diǎn)
上存在點(diǎn)![]() ,使
,使![]() ,求圓心
,求圓心![]() 的橫坐標(biāo)
的橫坐標(biāo)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com