Question

【題目】設函數f（x）=2ax2+（a+4）x+lnx．
（1）若f（x）在x= 處的切線與直線4x+y=0平行，求a的值；
（2）討論函數f（x）的單調區間；
（3）若函數y=f（x）的圖象與x軸交于A，B兩點，線段AB中點的橫坐標為x0 ， 證明f′（x0）＜0．

Answer 1

【答案】
（1）解：由題知f（x）=2ax2+（a+4）x+lnx，

則 ．

又∵f（x）的圖象在x= 處的切線與直線4x+y=0平行，

∴ ，即4a× + ×（a+4）+1=﹣1，

解得 a=﹣6．

（2）解：由（1）得， ，

由題知f（x）=2ax2+（a+4）x+lnx的定義域為（0，+∞），

由x＞0，得 ＞0．

①當a≥0時，對任意x＞0，f′（x）＞0，

∴此時函數f（x）的單調遞增區間為（0，+∞）．

②當a＜0時，令f′（x）=0，解得 ，

當 時，f′（x）＞0，當 時，f′（x）＜0，

此時，函數f（x）的單調遞增區間為（0， ），單調遞減區間為（ ，+∞）．

（3）解：不妨設A（x1，0），B（x2，0），且0＜x1＜x2，由（Ⅱ）知 a＜0，

于是要證f'（x）＜0成立，只需證： 即 ．

∵ ，①

，②

①﹣②得 ，

即 ，

∴ ，

故只需證 ，

即證明 ，

即證明 ，變形為 ，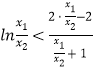

設 （0＜t＜1），令 ，

則 = ，

顯然當t＞0時，g′（t）≥0，當且僅當t=1時，g′（t）=0，

∴g（t）在（0，+∞）上是增函數．

又∵g（1）=0，

∴當t∈（0，1）時，g（t）＜0總成立，命題得證

【解析】（1）利用求導公式求出導數并化簡，由導數的幾何意義和題意可得f′（ ）=﹣4，解出a的值即可；（2）對導數因式分解后，再求出函數f（x）的定義域，然后在定義域內分a≥0，a＜0兩種情況，解不等式f′（x）＞0，f′（x）＜0可得函數的單調區間；（3）設出函數y=f（x）的圖象與x軸交于A，B兩點的橫坐標，利用分析法和根據（2）結論進行證明，根據要證明的結論和分析的過程，利用放縮法、換元法、構造函數法解答，再利用導數求出函數的最值，即可證明結論．
【考點精析】根據題目的已知條件，利用利用導數研究函數的單調性的相關知識可以得到問題的答案，需要掌握一般的,函數的單調性與其導數的正負有如下關系： 在某個區間內，(1)如果，那么函數在這個區間單調遞增；(2)如果，那么函數在這個區間單調遞減．