
【題目】已知函數![]() ,
, ![]() .
.
(1)求函數![]() 的極值;
的極值;
(2)若不等式![]() 對
對![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)答案見解析;(2) ![]() .
.
【解析】試題分析:(1)對函數求導得到![]()
![]() ,討論
,討論![]() 和0和1 的大小關系,在不同情況下求得導函數的正負即得到原函數的單調性,根據極值的概念得到結果;(2)設
和0和1 的大小關系,在不同情況下求得導函數的正負即得到原函數的單調性,根據極值的概念得到結果;(2)設![]()
![]() ,構造以上函數,研究函數的單調性,求得函數的最值,使得最小值大于等于0即可.
,構造以上函數,研究函數的單調性,求得函數的最值,使得最小值大于等于0即可.
解析:
(Ⅰ)![]() ,
,
![]()
![]() ,
,
∵![]() 的定義域為
的定義域為![]() .
.
①![]() 即
即![]() 時,
時, ![]() 在
在![]() 上遞減,
上遞減, ![]() 在
在![]() 上遞增,
上遞增,
![]() ,
, ![]() 無極大值.
無極大值.
②![]() 即
即![]() 時,
時, ![]() 在
在![]() 和
和![]() 上遞增,在
上遞增,在![]() 上遞減,
上遞減,
![]()
![]() ,
, ![]() .
.
③![]() 即
即![]() 時,
時, ![]() 在
在![]() 上遞增,
上遞增, ![]() 沒有極值.
沒有極值.
④![]() 即
即![]() 時,
時, ![]() 在
在![]() 和
和![]() 上遞增,
上遞增, ![]() 在
在![]() 上遞減,
上遞減,
∴![]() ,
, ![]()
![]() .
.
綜上可知: ![]() 時,
時, ![]() ,
, ![]() 無極大值;
無極大值;
![]() 時,
時, ![]()
![]() ,
, ![]() ;
;
![]() 時,
時, ![]() 沒有極值;
沒有極值;
![]() 時,
時, ![]() ,
, ![]()
![]() .
.
(Ⅱ)設![]()
![]() ,
,
![]() ,
,
設![]() ,則
,則![]() ,
, ![]() ,
, 
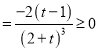 ,
,
∴![]() 在
在![]() 上遞增,∴
上遞增,∴![]() 的值域為
的值域為![]() ,
,
①當![]() 時,
時, ![]() ,
, ![]() 為
為![]() 上的增函數,
上的增函數,
∴![]() ,適合條件.
,適合條件.
②當![]() 時,∵
時,∵![]() ,∴不適合條件.
,∴不適合條件.
③當![]() 時,對于
時,對于![]() ,
, ![]() ,
,
令![]() ,
, ![]() ,
,
存在![]() ,使得
,使得![]() 時,
時, ![]() ,
,
∴![]() 在
在![]() 上單調遞減,
上單調遞減,
∴![]() ,
,
即在![]() 時,
時, ![]() ,∴不適合條件.
,∴不適合條件.
綜上, ![]() 的取值范圍為
的取值范圍為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為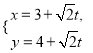 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,并使得它與直角坐標系
軸的正半軸為極軸建立極坐標系,并使得它與直角坐標系![]() 有相同的長度單位,曲線
有相同的長度單位,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 與直線
與直線![]() 交于
交于![]() 、
、![]() 兩點,且
兩點,且![]() 點的坐標為
點的坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區某農產品近幾年的產量統計如下表:

(1)根據表中數據,建立![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若近幾年該農產品每千克的價格![]() (單位:元)與年產量
(單位:元)與年產量![]() 滿足的函數關系式為
滿足的函數關系式為![]() ,且每年該農產品都能售完.
,且每年該農產品都能售完.
①根據(1)中所建立的回歸方程預測該地區![]() 年該農產品的產量;
年該農產品的產量;
②當![]() 為何值時,銷售額
為何值時,銷售額![]() 最大?
最大?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: 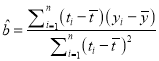 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場為了了解顧客的購物信息,隨機在商場收集了![]() 位顧客購物的相關數據如下表:
位顧客購物的相關數據如下表:
一次購物款(單位:元) |
|
|
|
|
|
顧客人數 |
|
|
|
|
|
統計結果顯示![]() 位顧客中購物款不低于
位顧客中購物款不低于![]() 元的顧客占
元的顧客占![]() ,該商場每日大約有
,該商場每日大約有![]() 名顧客,為了增加商場銷售額度,對一次購物不低于
名顧客,為了增加商場銷售額度,對一次購物不低于![]() 元的顧客發放紀念品.
元的顧客發放紀念品.
(Ⅰ)試確定![]() ,
, ![]() 的值,并估計每日應準備紀念品的數量;
的值,并估計每日應準備紀念品的數量;
(Ⅱ)現有![]() 人前去該商場購物,求獲得紀念品的數量
人前去該商場購物,求獲得紀念品的數量![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某大型水上樂園內有一塊矩形場地![]() 米,
米, ![]() 米,以
米,以![]() 為直徑的半圓
為直徑的半圓![]() 和半圓
和半圓![]() (半圓在矩形
(半圓在矩形![]() 內部)為兩個半圓形水上主題樂園,
內部)為兩個半圓形水上主題樂園, ![]() 都建有圍墻,游客只能從線段
都建有圍墻,游客只能從線段![]() 處進出該主題樂園.為了進一步提高經濟效益,水上樂園管理部門決定沿著
處進出該主題樂園.為了進一步提高經濟效益,水上樂園管理部門決定沿著![]() 修建不銹鋼護欄,沿著線段
修建不銹鋼護欄,沿著線段![]() 修建該主題樂園大門并設置檢票口,其中
修建該主題樂園大門并設置檢票口,其中![]() 分別為
分別為![]() 上的動點,
上的動點, ![]() ,且線段
,且線段![]() 與線段
與線段![]() 在圓心
在圓心![]() 和
和![]() 連線的同側.已知弧線部分的修建費用為
連線的同側.已知弧線部分的修建費用為![]() 元/米,直線部門的平均修建費用為
元/米,直線部門的平均修建費用為![]() 元/米.
元/米.

(1)若![]() 米,則檢票等候區域(其中陰影部分)面積為多少平方米?
米,則檢票等候區域(其中陰影部分)面積為多少平方米?
(2)試確定點![]() 的位置,使得修建費用最低.
的位置,使得修建費用最低.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家電公司根據銷售區域將銷售員分成![]() 兩組.2017年年初,公司根據銷售員的銷售業績分發年終獎,銷售員的銷售額(單位:十萬元)在區間
兩組.2017年年初,公司根據銷售員的銷售業績分發年終獎,銷售員的銷售額(單位:十萬元)在區間![]() 內對應的年終獎分別為2萬元,2.5萬元,3萬元,3.5萬元.已知200名銷售員的年銷售額都在區間
內對應的年終獎分別為2萬元,2.5萬元,3萬元,3.5萬元.已知200名銷售員的年銷售額都在區間![]() 內,將這些數據分成4組:
內,將這些數據分成4組: ![]() ,得到如下兩個頻率分布直方圖:
,得到如下兩個頻率分布直方圖:

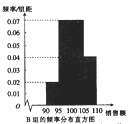
以上面數據的頻率作為概率,分別從![]() 組與
組與![]() 組的銷售員中隨機選取1位,記
組的銷售員中隨機選取1位,記![]() 分別表示
分別表示![]() 組與
組與![]() 組被選取的銷售員獲得的年終獎.
組被選取的銷售員獲得的年終獎.
(1)求![]() 的分布列及數學期;
的分布列及數學期;
(2)試問![]() 組與
組與![]() 組哪個組銷售員獲得的年終獎的平均值更高?為什么?
組哪個組銷售員獲得的年終獎的平均值更高?為什么?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市為鼓勵人們綠色出行,乘坐地鐵,地鐵公司決定按照乘客經過地鐵站的數量實施分段優惠政策,不超過![]() 站的地鐵票價如下表:
站的地鐵票價如下表:
乘坐站數 |
|
|
|
票價(元) |
|
|
|
現有甲、乙兩位乘客同時從起點乘坐同一輛地鐵,已知他們乘坐地鐵都不超過![]() 站,且他們各自在每個站下車的可能性是相同的.
站,且他們各自在每個站下車的可能性是相同的.
(1)若甲、乙兩人共付費![]() 元,則甲、乙下車方案共有多少種?
元,則甲、乙下車方案共有多少種?
(2)若甲、乙兩人共付費![]() 元,求甲比乙先到達目的地的概率.
元,求甲比乙先到達目的地的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com