
【題目】數學中有許多形狀優美、寓意美好的曲線,例如:四葉草曲線就是其中一種,其方程為![]() .給出下列四個結論:
.給出下列四個結論:
①曲線![]() 有四條對稱軸;
有四條對稱軸;
②曲線![]() 上的點到原點的最大距離為
上的點到原點的最大距離為![]() ;
;
③曲線![]() 第一象限上任意一點作兩坐標軸的垂線與兩坐標軸圍成的矩形面積最大值為
第一象限上任意一點作兩坐標軸的垂線與兩坐標軸圍成的矩形面積最大值為![]() ;
;
④四葉草面積小于![]() .
.
其中,所有正確結論的序號是( )

A.①②B.①③C.①③④D.①②④
【答案】C
【解析】
①利用![]() 之間的代換判斷出對稱軸的條數;②利用基本不等式求解出到原點的距離最大值;③將面積轉化為
之間的代換判斷出對稱軸的條數;②利用基本不等式求解出到原點的距離最大值;③將面積轉化為![]() 的關系式,然后根據基本不等式求解出最大值;④根據
的關系式,然后根據基本不等式求解出最大值;④根據![]() 滿足的不等式判斷出四葉草與對應圓的關系,從而判斷出面積是否小于
滿足的不等式判斷出四葉草與對應圓的關系,從而判斷出面積是否小于![]() .
.
①:當![]() 變為
變為![]() 時,
時, ![]() 不變,所以四葉草圖象關于
不變,所以四葉草圖象關于![]() 軸對稱;
軸對稱;
當![]() 變為
變為![]() 時,
時,![]() 不變,所以四葉草圖象關于
不變,所以四葉草圖象關于![]() 軸對稱;
軸對稱;
當![]() 變為
變為![]() 時,
時,![]() 不變,所以四葉草圖象關于
不變,所以四葉草圖象關于![]() 軸對稱;
軸對稱;
當![]() 變為
變為![]() 時,
時,![]() 不變,所以四葉草圖象關于
不變,所以四葉草圖象關于![]() 軸對稱;
軸對稱;
綜上可知:有四條對稱軸,故正確;
②:因為![]() ,所以
,所以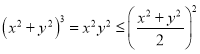 ,
,
所以![]() ,所以
,所以![]() ,取等號時
,取等號時![]() ,
,
所以最大距離為![]() ,故錯誤;
,故錯誤;
③:設任意一點![]() ,所以圍成的矩形面積為
,所以圍成的矩形面積為![]() ,
,
因為![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
取等號時![]() ,所以圍成矩形面積的最大值為
,所以圍成矩形面積的最大值為![]() ,故正確;
,故正確;
④:由②可知![]() ,所以四葉草包含在圓
,所以四葉草包含在圓![]() 的內部,
的內部,
因為圓的面積為:![]() ,所以四葉草的面積小于
,所以四葉草的面積小于![]() ,故正確.
,故正確.
故選:C.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某地區現有一個直角梯形水產養殖區ABCD,∠ABC=90°,AB∥CD,AB=800m,BC=1600m,CD=4000m,在點P處有一燈塔(如圖),且點P到BC,CD的距離都是1200m,現擬將養殖區ACD分成兩塊,經過燈塔P增加一道分隔網EF,在△AEF內試驗養殖一種新的水產品,當△AEF的面積最小時,對原有水產品養殖的影響最小.設AE=d.
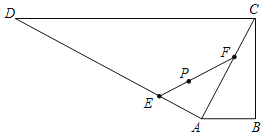
(1)若P是EF的中點,求d的值;
(2)求對原有水產品養殖的影響最小時的d的值,并求△AEF面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() ,離心率
,離心率![]() ,
,![]() 是橢圓的左頂點,
是橢圓的左頂點,![]() 是橢圓的左焦點,
是橢圓的左焦點,![]() ,直線
,直線![]() :
:![]() .
.
(1)求橢圓![]() 方程;
方程;
(2)直線![]() 過點
過點![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,直線
兩點,直線![]() 、
、![]() 分別與直線
分別與直線![]() 交于
交于![]() 、
、![]() 兩點,試問:以
兩點,試問:以![]() 為直徑的圓是否過定點,如果是,請求出定點坐標;如果不是,請說明理由.
為直徑的圓是否過定點,如果是,請求出定點坐標;如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在邊長為4的正方形![]() 中,
中,![]() 是
是![]() 的中點,
的中點,![]() 是
是![]() 的中點,現將三角形
的中點,現將三角形![]() 沿
沿![]() 翻折成如圖2所示的五棱錐
翻折成如圖2所示的五棱錐![]() .
.
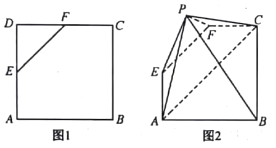
(1)求證:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={1,2,3,4,5,6,7,8,9),在集合A中任取三個元素,分別作為一個三位數的個位數,十位數和百位數,記這個三位數為a,現將組成a的三個數字按從小到大排成的三位數記為I(a),按從大到小排成的三位數記為D(a)(例如a=219,則I(a)=129,D(a)=921),閱讀如圖所示的程序框圖,運行相應的程序,任意輸入一個a,則輸出b的值為( )
A. 792 B. 693 C. 594 D. 495
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸的正半軸,建立平面直角坐標系,直線
軸的正半軸,建立平面直角坐標系,直線![]() 過點
過點![]() ,傾斜角為
,傾斜角為![]() .
.
(1)求曲線![]() 的直角坐標方程與直線l的參數方程;
的直角坐標方程與直線l的參數方程;
(2)設直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某搜索引擎廣告按照付費價格對搜索結果進行排名,點擊一次付費價格排名越靠前,被點擊的次數也可能會提高,已知某關鍵詞被甲、乙等多個公司競爭,其中甲、乙付費情況與每小時點擊量結果繪制成如下的折線圖.
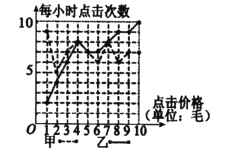
(1)試根據所給數據計算每小時點擊次數的均值方差并分析兩組數據的特征;
(2)若把乙公司設置的每次點擊價格為x,每小時點擊次數為y,則點(x,y)近似在一條直線附近.試根據前5次價格與每小時點擊次數的關系,求y關于x的回歸直線![]() .(附:回歸方程系數公式:
.(附:回歸方程系數公式: )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com