(本小題滿分13分)已知函數(shù)
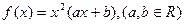
在
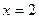
時有極值,其圖象在點
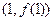
處的切線與直線
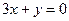
平行.(1)求
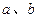
的值和函數(shù)
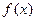
的單調(diào)區(qū)間;(2)若當
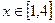
時,恒有
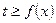
,試確定
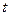
的取值范圍.
(Ⅰ)
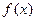
的單調(diào)遞增區(qū)間為:
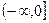
和
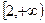
;單調(diào)遞減區(qū)間為:
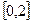
(Ⅱ)
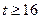
(1)
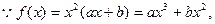
∴
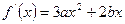
.
由已知可得:
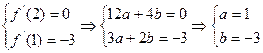
由
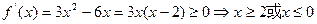


∴
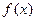
的單調(diào)遞增區(qū)間為:
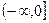
和
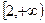
;單調(diào)遞減區(qū)間為:
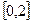
.
(2)
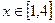
由(1)得:
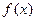
在
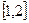
上單調(diào)遞減,在
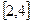
上單調(diào)遞增,
當
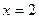
時取得極小值,又
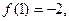
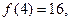
∴
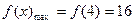
∴ 當
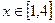
時,恒有
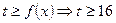
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:單選題
已知函數(shù)
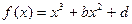
在(0,2)內(nèi)是減函數(shù),且2是方程
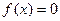
的根,則( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
若函數(shù) f(x)=
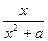
(a>0)在[1,+∞)上的最大值為
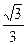
,則a的值為
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分14分)
設(shè)函數(shù)
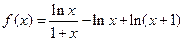
.
(Ⅰ)求
f(
x)的單調(diào)區(qū)間和極值;
(Ⅱ)是否存在實數(shù)
a,使得關(guān)于
x的不等式
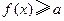
的解集為(0,+
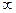
)?若存在,求
a的取值范圍;若不存在,試說明理由.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分14分)
設(shè)函數(shù)
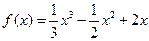
,
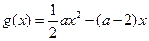
,
(1)對于任意實數(shù)
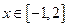
,
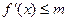
恒成立,求
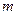
的最小值;
(2)若方程
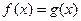
在區(qū)間
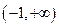
有三個不同的實根,求
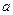
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)設(shè)

和

是函數(shù)

的兩個極值點。
(Ⅰ)求

和

的值;(Ⅱ)求

的單調(diào)區(qū)間
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
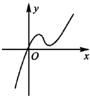
定義在R上的函數(shù)f(x)滿足f(4)=1,f′(x)為f(x)的導函數(shù),已知函數(shù)y=f′(x)的圖象如圖所示.若正數(shù)a,b滿足f(2a+b)<1,則
的取值范圍是( )
| A.(,2) | B.(-∞,)∪(3,+∞) | C.(,3) | D.(-∞,3) |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
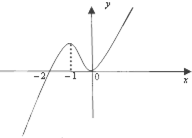
已知在R上可導的函數(shù)f(x)的圖象如圖所示,則不等式f(x)•f′(x)<0的解集為( )
| A.(-2,0) | B.(-∞,-2)∪(-1,0) | C.(-∞,-2)∪(0,+∞) | D.(-2,-1)∪(0,+∞) |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
若以曲線
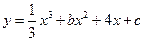
(c為實常數(shù))上任意一點為切點的切線的斜率恒為非負數(shù),則實數(shù)b的取值范圍為
。
查看答案和解析>>

 在
在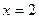 時有極值,其圖象在點
時有極值,其圖象在點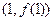 處的切線與直線
處的切線與直線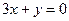 平行.(1)求
平行.(1)求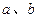 的值和函數(shù)
的值和函數(shù)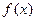 的單調(diào)區(qū)間;(2)若當
的單調(diào)區(qū)間;(2)若當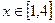 時,恒有
時,恒有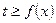 ,試確定
,試確定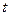 的取值范圍.
的取值范圍.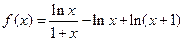 .
.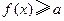 的解集為(0,+
的解集為(0,+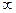 )?若存在,求a的取值范圍;若不存在,試說明理由.
)?若存在,求a的取值范圍;若不存在,試說明理由.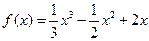 ,
,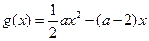 ,
,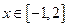 ,
,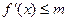 恒成立,求
恒成立,求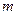 的最小值;
的最小值;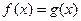 在區(qū)間
在區(qū)間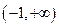 有三個不同的實根,求
有三個不同的實根,求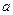 的取值范圍.
的取值范圍.
