
【題目】在一塊耕地上種植一種作物,每季種植成本為1000元,此作物的市場價格和這塊地上的產(chǎn)量均具有隨機性,且互不影響,其具體情況如下表:
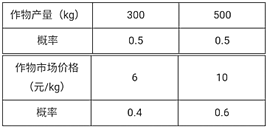
(1)設(shè)![]() 表示在這塊地上種植1季此作物的利潤,求
表示在這塊地上種植1季此作物的利潤,求![]() 的分布列;
的分布列;
(2)若在這塊地上連續(xù)3季種植此作物,求這3季中至少有2季的利潤不少于2000元的概率.
【答案】(1)分布列見解析;(2)![]() .
.
【解析】
試題(1)設(shè)![]() 表示事件“作物產(chǎn)量為300
表示事件“作物產(chǎn)量為300![]() ”,
”,![]() 表示事件“作物市場價格為6元
表示事件“作物市場價格為6元![]() ”
”
由題設(shè)得4000,2000,800,結(jié)合概率公式計算出對應的概率,得出分布列;
(2)設(shè)![]() 表示事件“第
表示事件“第![]() 季利潤不少于2000元”
季利潤不少于2000元”![]() ,由題意知:
,由題意知:![]() 相互獨立,由(1)知
相互獨立,由(1)知
![]()
![]() ,3季利潤均不少于2000元的概率為:
,3季利潤均不少于2000元的概率為:
![]() ,3季中有2季利潤不少于2000元的概率為:
,3季中有2季利潤不少于2000元的概率為:
![]() ,根據(jù)互斥事件概率的加法公式得:這3季中至少有2季的利潤不少于2000元的概率為:
,根據(jù)互斥事件概率的加法公式得:這3季中至少有2季的利潤不少于2000元的概率為:![]()
試題解析:(1)設(shè)![]() 表示事件“作物產(chǎn)量為300
表示事件“作物產(chǎn)量為300![]() ”,
”,![]() 表示事件“作物市場價格為6元
表示事件“作物市場價格為6元![]() ”
”
由題設(shè)知:![]() ,
,![]()
因為利潤=產(chǎn)量![]() 市場價格-成本
市場價格-成本
所以![]() 所以可能的取值為
所以可能的取值為
![]() ,
,![]()
![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() ,
,
所以![]() 的分布列為
的分布列為
| 4000 | 2000 | 800 |
| 0.3 | 0.5 | 0.2 |
(2)設(shè)![]() 表示事件“第
表示事件“第![]() 季利潤不少于2000元”
季利潤不少于2000元”![]() ,
,
由題意知:![]() 相互獨立,由(1)知
相互獨立,由(1)知
![]()
![]()
3季利潤均不少于2000元的概率為:
![]()
3季中有2季利潤不少于2000元的概率為:
![]()
所以,這3季中至少有2季的利潤不少于2000元的概率為:
![]()


科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標原點為極點,
為參數(shù)),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 的直角坐標方程;
的直角坐標方程;
(2)設(shè)點![]() 的坐標為
的坐標為![]() ,若點
,若點![]() 是曲線
是曲線![]() 截直線
截直線![]() 所得線段的中點,求
所得線段的中點,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】政府工作報告指出,2018年我國深入實施創(chuàng)新驅(qū)動發(fā)展戰(zhàn)略,創(chuàng)新能力和效率進一步提升;2019年要提升科技支撐能力,健全以企業(yè)為主體的產(chǎn)學研一體化創(chuàng)新機制.某企業(yè)為了提升行業(yè)核心競爭力,逐漸加大了科技投入;該企業(yè)連續(xù)6年來的科技投入![]() (百萬元)與收益
(百萬元)與收益![]() (百萬元)的數(shù)據(jù)統(tǒng)計如下:
(百萬元)的數(shù)據(jù)統(tǒng)計如下:
科技投入 | 2 | 4 | 6 | 8 | 10 | 12 |
收益 |
|
|
|
|
|
|
根據(jù)散點圖的特點,甲認為樣本點分布在指數(shù)曲線![]() 的周圍,據(jù)此他對數(shù)據(jù)進行了一些初步處理,如下表:
的周圍,據(jù)此他對數(shù)據(jù)進行了一些初步處理,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
其中![]() ,
,![]() .
.
(1)(i)請根據(jù)表中數(shù)據(jù),建立![]() 關(guān)于
關(guān)于![]() 的回歸方程(保留一位小數(shù));
的回歸方程(保留一位小數(shù));
(ii)根據(jù)所建立的回歸方程,若該企業(yè)想在下一年的收益達到2億,則科技投入的費用至少要多少(其中![]() )?
)?
(2)乙認為樣本點分布在二次曲線![]() 的周圍,并計算得回歸方程為
的周圍,并計算得回歸方程為![]() ,以及該回歸模型的相關(guān)指數(shù)
,以及該回歸模型的相關(guān)指數(shù)![]() ,試比較甲、乙兩位員工所建立的模型,誰的擬合效果更好.
,試比較甲、乙兩位員工所建立的模型,誰的擬合效果更好.
附:對于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() ,其回歸直線方程
,其回歸直線方程![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為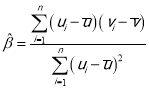 ,
,![]() ,相關(guān)指數(shù):
,相關(guān)指數(shù):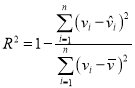 .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】計劃在某水庫建一座至多安裝3臺發(fā)電機的水電站,過去50年的水文資料顯示,水庫年入流量![]() (年入流量:一年內(nèi)上游來水與庫區(qū)降水之和.單位:億立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超過120的年份有35年,超過120的年份有5年.將年入流量在以上三段的頻率作為相應段的概率,并假設(shè)各年的年入流量相互獨立.
(年入流量:一年內(nèi)上游來水與庫區(qū)降水之和.單位:億立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超過120的年份有35年,超過120的年份有5年.將年入流量在以上三段的頻率作為相應段的概率,并假設(shè)各年的年入流量相互獨立.
(1)求未來4年中,至多1年的年入流量超過120的概率;
(2)水電站希望安裝的發(fā)電機盡可能運行,但每年發(fā)電機最多可運行臺數(shù)受年入流量![]() 限制,并有如下關(guān)系:
限制,并有如下關(guān)系:
年入流量 |
|
|
|
發(fā)電量最多可運行臺數(shù) | 1 | 2 | 3 |
若某臺發(fā)電機運行,則該臺年利潤為5000萬元;若某臺發(fā)電機未運行,則該臺年虧損800萬元,欲使水電站年總利潤的均值達到最大,應安裝發(fā)電機多少臺?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】工人在安裝一個正六邊形零件時,需要固定如圖所示的六個位置的螺絲,第一階段,首先隨意擰一個螺絲,接著擰它對角線上(距離它最遠的,下同)螺絲,再隨意擰第三個螺絲,第四個也擰它對角線上螺絲,第五個和第六個以此類推,但每個螺絲都不要擰死;第二階段,將每個螺絲擰死,但不能連續(xù)擰相鄰的2個螺絲.則不同的固定方式有________.
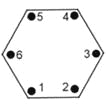
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】從批量較大的產(chǎn)品中隨機取出10件產(chǎn)品進行質(zhì)量檢測,若這批產(chǎn)品的不合格率為0.05,隨機變量![]() 表示這10件產(chǎn)品中的不合格產(chǎn)品的件數(shù).
表示這10件產(chǎn)品中的不合格產(chǎn)品的件數(shù).
(1)問:這10件產(chǎn)品中“恰好有2件不合格的概率![]() ”和“恰好有3件不合格的概率
”和“恰好有3件不合格的概率![]() ”哪個大?請說明理由;
”哪個大?請說明理由;
(2)求隨機變量![]() 的數(shù)學期望
的數(shù)學期望![]() .
.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com