
【題目】已知函數(shù)![]()
(1)當(dāng)a=-2時(shí),求函數(shù)f(x)的極值;
(2)若ln[e(x+1)]≥2- f(-x)對(duì)任意的x∈[0,+∞)成立,求實(shí)數(shù)a的取值范圍.
【答案】(1)不存在極大值,極小值為![]() (2)
(2)![]()
【解析】
(1)將![]() 代入函數(shù)解析式,求得導(dǎo)函數(shù)
代入函數(shù)解析式,求得導(dǎo)函數(shù)![]() 后結(jié)合函數(shù)
后結(jié)合函數(shù)![]() 的單調(diào)區(qū)間,求得
的單調(diào)區(qū)間,求得![]() 的極值.(2)化簡(jiǎn)題目所給不等式為
的極值.(2)化簡(jiǎn)題目所給不等式為![]() 對(duì)任意
對(duì)任意![]() 成立,構(gòu)造函數(shù)
成立,構(gòu)造函數(shù)![]() ,利用導(dǎo)數(shù)研究
,利用導(dǎo)數(shù)研究![]() 的單調(diào)性、最值,由此求得
的單調(diào)性、最值,由此求得![]() 的取值范圍.
的取值范圍.
(1)當(dāng)![]() 時(shí),
時(shí),![]() ,則
,則![]() ,令
,令![]() ,解得
,解得![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 遞減,當(dāng)
遞減,當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 遞增,所以
遞增,所以![]() 在
在![]() 處取得極小值
處取得極小值![]() ,無(wú)極大值.
,無(wú)極大值.
(2)由于![]() ,所以
,所以![]() ,又因?yàn)?/span>
,又因?yàn)?/span>![]() 對(duì)任意的
對(duì)任意的![]() 成立,化簡(jiǎn)得
成立,化簡(jiǎn)得![]() 對(duì)任意
對(duì)任意![]() 成立.構(gòu)造函數(shù)
成立.構(gòu)造函數(shù)![]()
![]() ,
,![]() ,令
,令![]() ,即
,即![]() ,構(gòu)造函數(shù)
,構(gòu)造函數(shù)![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,所以
,所以![]() 在
在![]() 上遞增,當(dāng)
上遞增,當(dāng)![]() 時(shí),
時(shí),![]() .
.
當(dāng)![]() 即
即![]() 時(shí),
時(shí),![]() ,此時(shí)
,此時(shí)![]() 在
在![]() 上遞增,
上遞增,![]() 符合題意.
符合題意.
當(dāng)![]() 即
即![]() 時(shí),存在唯一實(shí)數(shù)
時(shí),存在唯一實(shí)數(shù)![]() ,使
,使![]() ,且當(dāng)
,且當(dāng)![]() 時(shí),
時(shí),![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,而
,而![]() ,故當(dāng)
,故當(dāng)![]() 時(shí),
時(shí),![]() 不符合題意.
不符合題意.
綜上所述,實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]()


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】日晷是中國(guó)古代用來(lái)測(cè)定時(shí)間的儀器,利用與晷面垂直的晷針投射到晷面的影子來(lái)測(cè)定時(shí)間.把地球看成一個(gè)球(球心記為O),地球上一點(diǎn)A的緯度是指OA與地球赤道所在平面所成角,點(diǎn)A處的水平面是指過(guò)點(diǎn)A且與OA垂直的平面.在點(diǎn)A處放置一個(gè)日晷,若晷面與赤道所在平面平行,點(diǎn)A處的緯度為北緯40°,則晷針與點(diǎn)A處的水平面所成角為( )

A.20°B.40°
C.50°D.90°
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
,![]() 為
為![]() 的導(dǎo)函數(shù).
的導(dǎo)函數(shù).
(Ⅰ)當(dāng)![]() 時(shí),
時(shí),
(i)求曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(ii)求函數(shù)![]() 的單調(diào)區(qū)間和極值;
的單調(diào)區(qū)間和極值;
(Ⅱ)當(dāng)![]() 時(shí),求證:對(duì)任意的
時(shí),求證:對(duì)任意的![]() ,且
,且![]() ,有
,有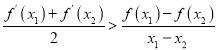 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,E是
,E是![]() 的中點(diǎn).現(xiàn)將
的中點(diǎn).現(xiàn)將![]() 沿
沿![]() 翻折,使點(diǎn)A移動(dòng)至平面
翻折,使點(diǎn)A移動(dòng)至平面![]() 外的點(diǎn)P.
外的點(diǎn)P.
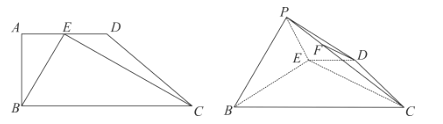
(1)若![]() ,求證:
,求證:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),討論
時(shí),討論![]() 極值點(diǎn)的個(gè)數(shù);
極值點(diǎn)的個(gè)數(shù);
(2)若函數(shù)![]() 有兩個(gè)零點(diǎn),求
有兩個(gè)零點(diǎn),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】函數(shù)f(x)=Asin(x+)(A>0,>0,0<<)的部分圖象如圖所示,又函數(shù)g(x)=f(x+![]() ).
).
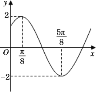
(1)求函數(shù)g(x)的單調(diào)增區(qū)間;
(2)設(shè)![]() ABC的內(nèi)角ABC的對(duì)邊分別為abc,又c=
ABC的內(nèi)角ABC的對(duì)邊分別為abc,又c=![]() ,且銳角C滿(mǎn)足g(C)= -1,若sinB=2sinA,,求ABC的面積.
,且銳角C滿(mǎn)足g(C)= -1,若sinB=2sinA,,求ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,且曲線
,且曲線![]() 在
在![]() 處的切線斜率為1.
處的切線斜率為1.
(1)求實(shí)數(shù)![]() 的值;
的值;
(2)證明:當(dāng)![]() 時(shí),
時(shí),![]() ;
;
(3)若數(shù)列![]() 滿(mǎn)足
滿(mǎn)足![]() ,且
,且![]() ,證明:
,證明:![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了治療某種疾病,某科研機(jī)構(gòu)研制了甲、乙兩種新藥,為此進(jìn)行白鼠試驗(yàn).試驗(yàn)方案如下:每一輪選取兩只白鼠對(duì)藥效進(jìn)行對(duì)比試驗(yàn).對(duì)于兩只白鼠,隨機(jī)選一只施以甲藥,另一只施以乙藥一輪的治療結(jié)果得出后,再安排下一輪試驗(yàn).4輪試驗(yàn)后,就停止試驗(yàn).甲、乙兩種藥的治愈率分別是![]() 和
和![]() .
.
(1)若![]() ,求2輪試驗(yàn)后乙藥治愈的白鼠比甲藥治愈的白鼠多1只的概率;
,求2輪試驗(yàn)后乙藥治愈的白鼠比甲藥治愈的白鼠多1只的概率;
(2)已知A公司打算投資甲、乙這兩種新藥的試驗(yàn)耗材費(fèi)用,甲藥和乙藥一次試驗(yàn)耗材花費(fèi)分別為3千元和![]() 千元,每輪試驗(yàn)若甲、乙兩種藥都治愈或都沒(méi)有治愈,則該科研機(jī)構(gòu)和A公司各承擔(dān)該輪試驗(yàn)耗材總費(fèi)用的50%;若甲藥治愈,乙藥未治愈,則A公司承擔(dān)該輪試驗(yàn)耗材總費(fèi)用的75%,其余由科研機(jī)構(gòu)承擔(dān),若甲藥未治愈,乙藥治愈,則A公司承擔(dān)該輪試驗(yàn)耗材總費(fèi)用的25%,其余由科研機(jī)構(gòu)承擔(dān).以A公司每輪支付試驗(yàn)耗材費(fèi)用的期望為標(biāo)準(zhǔn),求A公司4輪試驗(yàn)結(jié)束后支付試驗(yàn)耗材最少費(fèi)用為多少元?
千元,每輪試驗(yàn)若甲、乙兩種藥都治愈或都沒(méi)有治愈,則該科研機(jī)構(gòu)和A公司各承擔(dān)該輪試驗(yàn)耗材總費(fèi)用的50%;若甲藥治愈,乙藥未治愈,則A公司承擔(dān)該輪試驗(yàn)耗材總費(fèi)用的75%,其余由科研機(jī)構(gòu)承擔(dān),若甲藥未治愈,乙藥治愈,則A公司承擔(dān)該輪試驗(yàn)耗材總費(fèi)用的25%,其余由科研機(jī)構(gòu)承擔(dān).以A公司每輪支付試驗(yàn)耗材費(fèi)用的期望為標(biāo)準(zhǔn),求A公司4輪試驗(yàn)結(jié)束后支付試驗(yàn)耗材最少費(fèi)用為多少元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】函數(shù)![]() ,
,![]() .
.
(1)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若![]() 在
在![]() 上恒成立,求實(shí)數(shù)
上恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com