【題目】已知
R，函數(shù)
=
.
（1）當(dāng)
時，解不等式>1；
（2）若關(guān)于
的方程+
=0的解集中恰有一個元素，求
的值；
（3）設(shè)
>0，若對任意
，函數(shù)在區(qū)間
上的最大值與最小值的差不超過1，求的取值范圍.
【答案】（1）
；（2）
或
；（3）
.
【解析】
試題分析：（1）利用已知條件，將
代入，解不等式，求出
的取值范圍；（2）首先分情況進(jìn)行討論，利用僅有一解，即
和的兩種情況進(jìn)行討論；（3）利用函數(shù)
的單調(diào)性，最大值和最小值，將不等式進(jìn)行轉(zhuǎn)換和化簡從而求出
的取值范圍.
試題解析：（1）由
得
解得
（2）方程
的解集中恰有一個元素.
等價于
僅有一解，
等價于
僅有一解，
當(dāng)
時，
，符合題意；
當(dāng)
時，
，解得
綜上：或
（3）當(dāng)
時，
，
，
所以在
上單調(diào)遞減.
函數(shù)在區(qū)間
上的最大值與最小值分別為
，
.
即
，對任意
成立.
因為
，所以函數(shù)
在區(qū)間
上單調(diào)遞增，
所以
時，
有最小值
，由
，得
.1
故
的取值范圍為.
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在三棱錐
中，平面
平面
，
為等邊三角形，
且
，
，
分別為
，
的中點．
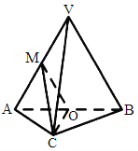
（I）求證：
平面
；
（II）求證：平面
平面
；
（III）求三棱錐
的體積．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某投資公司計劃投資A，B兩種金融產(chǎn)品，根據(jù)市場調(diào)查與預(yù)測，A產(chǎn)品的利潤y1與投資金額x的函數(shù)關(guān)系為y1＝18－
，B產(chǎn)品的利潤y2與投資金額x的函數(shù)關(guān)系為y2＝
(注：利潤與投資金額單位：萬元).
(1)該公司已有100萬元資金，并全部投入A，B兩種產(chǎn)品中，其中x萬元資金投入A產(chǎn)品，試把A，B兩種產(chǎn)品利潤總和表示為x的函數(shù)，并寫出定義域；
(2)在（1）的條件下，試問：怎樣分配這100萬元資金，才能使公司獲得最大利潤？其最大利潤為多少萬元？
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系
中，已知圓
過坐標(biāo)原點
且圓心在曲線
上．
(1)若圓分別與
軸、
軸交于點
、
(不同于原點)，求證：
的面積為定值；
(2)設(shè)直線
與圓交于不同的兩點
，且
，求圓的方程；
(3)設(shè)直線
與(2)中所求圓交于點
、
， 
為直線
上的動點，直線
，
與圓的另一個交點分別為
，
，且
，
在直線
異側(cè)，求證：直線
過定點，并求出定點坐標(biāo)．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
.
（Ⅰ）談?wù)摵瘮?shù)的單調(diào)性；
（Ⅱ）若函數(shù)
在區(qū)間
內(nèi)任取有兩個不相等的實數(shù)
，
，不等式
恒成立，求
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某高中有高一新生500名，分成水平相同的
兩類教學(xué)實驗，為對比教學(xué)效果，現(xiàn)用分層抽樣的方法從兩類學(xué)生中分別抽取了40人，60人進(jìn)行測試
（1）求該學(xué)校高一新生兩類學(xué)生各多少人？
（2）經(jīng)過測試，得到以下三個數(shù)據(jù)圖表：
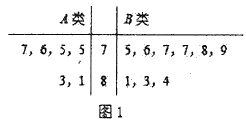
圖1：75分以上兩類參加測試學(xué)生成績的莖葉圖
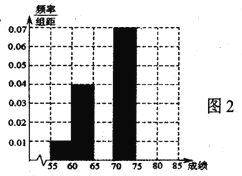
圖2：100名測試學(xué)生成績的頻率分布直方圖
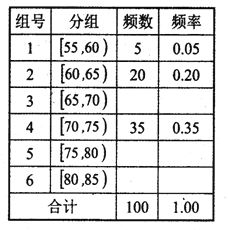
下圖表格：100名學(xué)生成績分布表：
①先填寫頻率分布表中的六個空格，然后將頻率分布直方圖（圖2）補(bǔ)充完整；
②該學(xué)校擬定從參加考試的79分以上（含79分）的
類學(xué)生中隨機(jī)抽取2人代表學(xué)校參加市比賽，求抽到的2人分?jǐn)?shù)都在80分以上的概率.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
為奇函數(shù)，且相鄰兩對稱軸間的距離為
.
（Ⅰ）當(dāng)
時，求
的單調(diào)遞減區(qū)間；
（Ⅱ）將函數(shù)
的圖象沿
軸方向向右平移
個單位長度，再把橫坐標(biāo)縮短到原來的
（縱坐標(biāo)不變），
得到函數(shù)
的圖象.當(dāng)
時，求函數(shù)
的值域.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)p:實數(shù)x滿足
,其中
,命題
實數(shù)
滿足
|x-3|≤1 .
(1)若
且
為真，求實數(shù)的取值范圍；
(2)若
是
的充分不必要條件,求實數(shù)a的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)函數(shù)
．
（Ⅰ）求曲線
在點
處的切線方程；
（Ⅱ）若
對
恒成立，求實數(shù)
的取值范圍；
（Ⅲ）求整數(shù)
的值，使函數(shù)
在區(qū)間
上有零點．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com