
【題目】已知函數(shù)![]() .
.
(Ⅰ)解不等式: ![]() ;
;
(Ⅱ)已知![]() ,若對(duì)任意的
,若對(duì)任意的![]() ,不等式
,不等式![]() 恒成立,求正數(shù)
恒成立,求正數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(I)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)由題意得不等式為![]() ,然后根據(jù)分類討論的方法,去掉絕對(duì)值后解不等式組即可.(Ⅱ)根據(jù)題意先得到
,然后根據(jù)分類討論的方法,去掉絕對(duì)值后解不等式組即可.(Ⅱ)根據(jù)題意先得到![]() ,故由題意得
,故由題意得![]() 恒成立,分類討論去掉絕對(duì)值后可得所求范圍.
恒成立,分類討論去掉絕對(duì)值后可得所求范圍.
(Ⅰ)由題意得不等式為![]() .
.
①當(dāng)![]() 時(shí),原不等式化為
時(shí),原不等式化為![]() ,解得
,解得![]() ,不合題意;
,不合題意;
②當(dāng)![]() 時(shí),原不等式化為
時(shí),原不等式化為![]() ,解得
,解得![]() ,∴
,∴![]() ;
;
③當(dāng)![]() 時(shí),原不等式化為
時(shí),原不等式化為![]() ,解得
,解得![]() ,∴
,∴![]() .
.
綜上可得![]()
∴原不等式的解集為![]() .
.
(Ⅱ)∵![]() ,
,
∴![]() .
.
當(dāng)且僅當(dāng)![]() 且
且![]() ,即
,即![]() 時(shí)等號(hào)成立,
時(shí)等號(hào)成立,
∴![]() .
.
由題意得![]() 恒成立,
恒成立,
①當(dāng)![]() 時(shí),可得
時(shí),可得![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
∴![]() ,
,
由![]() ,可得上式顯然成立;
,可得上式顯然成立;
②當(dāng)![]() 時(shí),可得
時(shí),可得![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
∵![]() ,∴
,∴![]() ;
;
③當(dāng)![]() 時(shí),可得
時(shí),可得![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
∴![]() .
.
綜上可得![]() ,
,
∴故![]() 的取值范圍是
的取值范圍是![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】點(diǎn)![]() 、
、![]() 、
、![]() 分別是正方體
分別是正方體![]() 的棱
的棱![]() ,
,![]() ,
,![]() 的中點(diǎn),則下列命題中的真命題是__________(寫出所有真命題的序號(hào)).
的中點(diǎn),則下列命題中的真命題是__________(寫出所有真命題的序號(hào)).
①以正方體的頂點(diǎn)為頂點(diǎn)的三棱錐的四個(gè)面中最多可以四個(gè)面都是直角三角形;
②點(diǎn)![]() 在直線
在直線![]() 上運(yùn)動(dòng)時(shí),總有
上運(yùn)動(dòng)時(shí),總有![]() ;
;
③點(diǎn)![]() 在直線
在直線![]() 上運(yùn)動(dòng)時(shí),三棱錐
上運(yùn)動(dòng)時(shí),三棱錐![]() 的體積是定值;
的體積是定值;
④若![]() 是正方體的面
是正方體的面![]() ,(含邊界)內(nèi)一動(dòng)點(diǎn),且點(diǎn)
,(含邊界)內(nèi)一動(dòng)點(diǎn),且點(diǎn)![]() 到點(diǎn)
到點(diǎn)![]() 和
和![]() 的距離相等,則點(diǎn)
的距離相等,則點(diǎn)![]() 的軌跡是一條線段.
的軌跡是一條線段.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】![]() 是衡量空氣污染程度的一個(gè)指標(biāo),為了了解
是衡量空氣污染程度的一個(gè)指標(biāo),為了了解![]() 市空氣質(zhì)量情況,從
市空氣質(zhì)量情況,從![]() 年每天的
年每天的![]() 值的數(shù)據(jù)中隨機(jī)抽取
值的數(shù)據(jù)中隨機(jī)抽取![]() 天的數(shù)據(jù),其頻率分布直方圖如圖所示.將
天的數(shù)據(jù),其頻率分布直方圖如圖所示.將![]() 值劃分成區(qū)間
值劃分成區(qū)間![]() 、
、![]() 、
、![]() 、
、![]() ,分別稱為一級(jí)、二級(jí)、三級(jí)和四級(jí),統(tǒng)計(jì)時(shí)用頻率估計(jì)概率 .
,分別稱為一級(jí)、二級(jí)、三級(jí)和四級(jí),統(tǒng)計(jì)時(shí)用頻率估計(jì)概率 .

(1)根據(jù)![]() 年的數(shù)據(jù)估計(jì)該市在
年的數(shù)據(jù)估計(jì)該市在![]() 年中空氣質(zhì)量為一級(jí)的天數(shù);
年中空氣質(zhì)量為一級(jí)的天數(shù);
(2)如果![]() 市對(duì)環(huán)境進(jìn)行治理,經(jīng)治理后,每天
市對(duì)環(huán)境進(jìn)行治理,經(jīng)治理后,每天![]() 值
值![]() 近似滿足正態(tài)分布
近似滿足正態(tài)分布![]() ,求經(jīng)過(guò)治理后的
,求經(jīng)過(guò)治理后的![]() 值的均值下降率.
值的均值下降率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】拋物線![]() 的焦點(diǎn)為
的焦點(diǎn)為![]() ,準(zhǔn)線為
,準(zhǔn)線為![]() ,若
,若![]() 為拋物線上第一象限的一動(dòng)點(diǎn),過(guò)
為拋物線上第一象限的一動(dòng)點(diǎn),過(guò)![]() 作
作![]() 的垂線交準(zhǔn)線
的垂線交準(zhǔn)線![]() 于點(diǎn)
于點(diǎn)![]() ,交拋物線于
,交拋物線于![]() 兩點(diǎn).
兩點(diǎn).
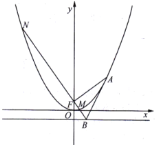
(Ⅰ)求證:直線![]() 與拋物線相切;
與拋物線相切;
(Ⅱ)若點(diǎn)![]() 滿足
滿足![]() ,求此時(shí)點(diǎn)
,求此時(shí)點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】現(xiàn)要完成下列三項(xiàng)抽樣調(diào)查:①從![]() 罐奶粉中抽取
罐奶粉中抽取![]() 罐進(jìn)行食品安全衛(wèi)生檢查;②高二年級(jí)有
罐進(jìn)行食品安全衛(wèi)生檢查;②高二年級(jí)有![]() 名學(xué)生,為調(diào)查學(xué)生的學(xué)習(xí)情況抽取一個(gè)容量為
名學(xué)生,為調(diào)查學(xué)生的學(xué)習(xí)情況抽取一個(gè)容量為![]() 的樣本;③從某社區(qū)
的樣本;③從某社區(qū)![]() 戶高收入家庭,
戶高收入家庭,![]() 戶中等收入家庭,
戶中等收入家庭,![]() 戶低收入家庭中選出
戶低收入家庭中選出![]() 戶進(jìn)行消費(fèi)水平調(diào)查.以下各調(diào)查方法較為合理的是( )
戶進(jìn)行消費(fèi)水平調(diào)查.以下各調(diào)查方法較為合理的是( )
A.①系統(tǒng)抽樣,②簡(jiǎn)單隨機(jī)抽樣,③分層抽樣
B.①簡(jiǎn)單隨機(jī)抽樣,②分層抽樣,③系統(tǒng)抽樣
C.①分層抽樣,②系統(tǒng)抽樣,③簡(jiǎn)單隨機(jī)抽樣
D.①簡(jiǎn)單隨機(jī)抽樣,②系統(tǒng)抽樣,③分層抽樣
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】綠水青山就是金山銀山.某山村為做好水土保持,退耕還林,在本村的山坡上種植水果,并推出山村游等旅游項(xiàng)目.為預(yù)估今年7月份游客購(gòu)買水果的情況,隨機(jī)抽樣統(tǒng)計(jì)了去年7月份100名游客的購(gòu)買金額.分組如下:![]() ,
,![]() ,
,![]()
![]() ,得到如圖所示的頻率分布直方圖:
,得到如圖所示的頻率分布直方圖:
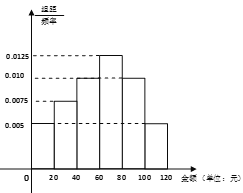
(1)請(qǐng)用抽樣的數(shù)據(jù)估計(jì)今年7月份游客人均購(gòu)買水果的金額(同一組中的數(shù)據(jù)用該組區(qū)間中點(diǎn)作代表).
(2)若把去年7月份購(gòu)買水果不低于80元的游客,稱為“水果達(dá)人”. 填寫下面列聯(lián)表,并根據(jù)列聯(lián)表判斷是否有95%的把握認(rèn)為“水果達(dá)人”與性別有關(guān)系?
水果達(dá)人 | 非水果達(dá)人 | 合計(jì) | |
男 | 10 | ||
女 | 30 | ||
合計(jì) |
(3)為吸引顧客,商家特推出兩種促銷方案.方案一:每滿80元可立減10元;方案二:金額超過(guò)80元可抽獎(jiǎng)三次,每次中獎(jiǎng)的概率為![]() ,且每次抽獎(jiǎng)互不影響,中獎(jiǎng)1次打9折,中獎(jiǎng)2次打8折,中獎(jiǎng)3次打7折.若每斤水果10元,你打算購(gòu)買12斤水果,請(qǐng)從實(shí)際付款金額的數(shù)學(xué)期望的角度分析應(yīng)該選擇哪種優(yōu)惠方案.
,且每次抽獎(jiǎng)互不影響,中獎(jiǎng)1次打9折,中獎(jiǎng)2次打8折,中獎(jiǎng)3次打7折.若每斤水果10元,你打算購(gòu)買12斤水果,請(qǐng)從實(shí)際付款金額的數(shù)學(xué)期望的角度分析應(yīng)該選擇哪種優(yōu)惠方案.
附:參考公式和數(shù)據(jù):![]() ,
,![]() .臨界值表:
.臨界值表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】畫糖是一種以糖為材料在石板上進(jìn)行造型的民間藝術(shù),常見于公園與旅游景點(diǎn).某師傅制作了一種新造型糖畫,為了進(jìn)行合理定價(jià)先進(jìn)性試銷售,其單價(jià)![]() (元)與銷量
(元)與銷量![]() (個(gè))相關(guān)數(shù)據(jù)如下表:
(個(gè))相關(guān)數(shù)據(jù)如下表:

(1)已知銷量![]() 與單價(jià)
與單價(jià)![]() 具有線性相關(guān)關(guān)系,求
具有線性相關(guān)關(guān)系,求![]() 關(guān)于
關(guān)于![]() 的線性相關(guān)方程;
的線性相關(guān)方程;
(2)若該新造型糖畫每個(gè)的成本為![]() 元,要使得進(jìn)入售賣時(shí)利潤(rùn)最大,請(qǐng)利用所求的線性相關(guān)關(guān)系確定單價(jià)應(yīng)該定為多少元?(結(jié)果保留到整數(shù))
元,要使得進(jìn)入售賣時(shí)利潤(rùn)最大,請(qǐng)利用所求的線性相關(guān)關(guān)系確定單價(jià)應(yīng)該定為多少元?(結(jié)果保留到整數(shù))
參考公式:線性回歸方程![]() 中斜率和截距最小二乘法估計(jì)計(jì)算公式:
中斜率和截距最小二乘法估計(jì)計(jì)算公式:

![]() .參考數(shù)據(jù):
.參考數(shù)據(jù):![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某工廠的![]() ,
,![]() ,
,![]() 三個(gè)不同車間生產(chǎn)同一產(chǎn)品的數(shù)量(單位:件)如下表所示.質(zhì)檢人員用分層抽樣的方法從這些產(chǎn)品中共抽取6件樣品進(jìn)行檢測(cè):
三個(gè)不同車間生產(chǎn)同一產(chǎn)品的數(shù)量(單位:件)如下表所示.質(zhì)檢人員用分層抽樣的方法從這些產(chǎn)品中共抽取6件樣品進(jìn)行檢測(cè):
車間 |
|
|
|
數(shù)量 | 50 | 150 | 100 |
(1)求這6件樣品中來(lái)自![]() ,
,![]() ,
,![]() 各車間產(chǎn)品的數(shù)量;
各車間產(chǎn)品的數(shù)量;
(2)若在這6件樣品中隨機(jī)抽取2件進(jìn)行進(jìn)一步檢測(cè),求這2件產(chǎn)品來(lái)自相同車間的概率.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com