
�O(sh��)�E�AC1: +
+ =1(a>b>0),���タ(xi��n)C2:x2+by=b2.
=1(a>b>0),���タ(xi��n)C2:x2+by=b2.
(1)��C2��(j��ng)�^(gu��)C1�ăɂ�(g��)���c(di��n),��C1���x����;
(2)�O(sh��)A(0,b),Q��3 ,
, b��,��M,N��C1�cC2����y�S�ϵăɂ�(g��)���c(di��n),����AMN�Ĵ��Ğ�B��0,
b��,��M,N��C1�cC2����y�S�ϵăɂ�(g��)���c(di��n),����AMN�Ĵ��Ğ�B��0,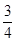 b��,�ҡ�QMN��������C2��,��E�AC1�͒��タ(xi��n)C2�ķ���.
b��,�ҡ�QMN��������C2��,��E�AC1�͒��タ(xi��n)C2�ķ���.
��1�� ��2��
��2��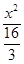 +
+ =1 x2+2y=4
=1 x2+2y=4
������:(1)��?y��n)钁�タ(xi��n)C2��(j��ng)�^(gu��)�E�AC1�ăɂ�(g��)���c(di��n)F1(-c,0),F2(c,0),
�ɵ�c2=b2,
��a2=b2+c2=2c2,
��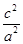 =
= ,
,
���ԙE�AC1���x����e= .
.
(2)���}�O(sh��)��֪M,N�P(gu��n)��y�S��(du��)�Q(ch��ng),
�O(sh��)M(-x1,y1),N(x1,y1)(x1>0),
�t�ɡ�AMN�Ĵ��Ğ�B,��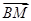 ��
��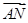 =0.
=0.
����-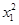 +��y1-
+��y1-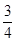 b��(y1-b)=0.��
b��(y1-b)=0.��
�����c(di��n)N(x1,y1)��C2��,
����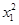 +by1=b2.��
+by1=b2.��
�ɢ٢ڵ�y1=-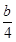 ��y1=b(��ȥ),
��y1=b(��ȥ),
����x1= b,
b,
��M��- b,-
b,-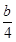 ��,N��
��,N�� b,-
b,-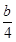 ��,
��,
���ԡ�QMN����������(bi��o)�飨 ,
,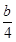 ��.
��.
��������C2�ϵ�3+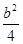 =b2,
=b2,
����b=2,
M��- ,-
,- ��,N��
��,N�� ,-
,- ��.
��.
����?y��n)�M,N��C1��,
����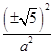 +
+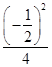 =1,
=1,
���a2=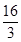 .
.
���ԙE�AC1�ķ��̞�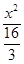 +
+ =1.
=1.
���タ(xi��n)C2�ķ��̞�x2+2y=4.


 �����یW(xu��)���̲���ȫ���xϵ�д�
�����یW(xu��)���̲���ȫ���xϵ�д� �����n�r(sh��)�����I(y��)����ϵ�д�
�����n�r(sh��)�����I(y��)����ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A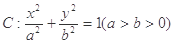 �ăɽ��c(di��n)��
�ăɽ��c(di��n)�� �S��, �҃ɽ��c(di��n)�c���S��һ��(g��)��c(di��n)���B��(xi��n)��(g��u)��б߅�L(zh��ng)��2�ĵ���ֱ��������
�S��, �҃ɽ��c(di��n)�c���S��һ��(g��)��c(di��n)���B��(xi��n)��(g��u)��б߅�L(zh��ng)��2�ĵ���ֱ��������
��1����E�A�ķ��̣�
��2���^(gu��)�c(di��n)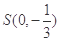 �Ą�(d��ng)ֱ��(xi��n)
�Ą�(d��ng)ֱ��(xi��n)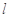 ���E�AC��A��B���c(di��n)��ԇ��(w��n)��������(bi��o)ƽ�����Ƿ����һ��(g��)���c(di��n)Q��ʹ����AB��ֱ���ĈA���^(gu��)�c(di��n)Q?����������c(di��n)Q������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)������
���E�AC��A��B���c(di��n)��ԇ��(w��n)��������(bi��o)ƽ�����Ƿ����һ��(g��)���c(di��n)Q��ʹ����AB��ֱ���ĈA���^(gu��)�c(di��n)Q?����������c(di��n)Q������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪������ԭ�c(di��n)���p����(xi��n) ���ҽ��c(di��n)��
���ҽ��c(di��n)��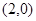 ����(sh��)�S�L(zh��ng)
����(sh��)�S�L(zh��ng)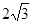 .
.
��1�����p����(xi��n)�ķ���
��2����ֱ��(xi��n)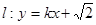 �c�p����(xi��n)���Ѓɂ�(g��)��ͬ�Ľ��c(di��n)
�c�p����(xi��n)���Ѓɂ�(g��)��ͬ�Ľ��c(di��n) ����
���� ���J��(����
���J��(���� ��ԭ�c(di��n))����
��ԭ�c(di��n))���� ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�O(sh��)���A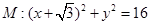 ����(d��ng)�A
����(d��ng)�A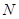 �^(gu��)�c(di��n)
�^(gu��)�c(di��n)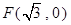 ���c�A
���c�A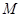 ���У�ӛ��(d��ng)�A
���У�ӛ��(d��ng)�A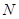 �A��
�A��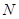 ��܉�E��
��܉�E��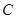 .
.
��1����܉�E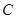 �ķ��̣�
�ķ��̣�
��2����֪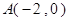 ���^(gu��)���c(di��n)
���^(gu��)���c(di��n)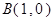 �Ą�(d��ng)ֱ��(xi��n)
�Ą�(d��ng)ֱ��(xi��n)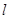 ��܉�E
��܉�E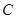 ��
��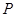 ��
��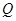 ���c(di��n)��
���c(di��n)��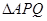 ������
�����Ğ�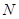 ����ֱ��(xi��n)
����ֱ��(xi��n)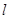 ��б�ʞ�
��б�ʞ�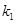 ��ֱ��(xi��n)
��ֱ��(xi��n)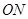 ��б�ʞ�
��б�ʞ�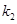 �����C��
�����C��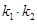 �鶨ֵ��
�鶨ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�A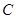 ��������ԭ�c(di��n)�����c(di��n)��
��������ԭ�c(di��n)�����c(di��n)��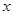 �S�ϣ��L(zh��ng)�S�L(zh��ng)�Ƕ��S�L(zh��ng)��
�S�ϣ��L(zh��ng)�S�L(zh��ng)�Ƕ��S�L(zh��ng)��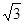 ��������һ�c(di��n)���ҽ��c(di��n)����̾��x��
��������һ�c(di��n)���ҽ��c(di��n)����̾��x��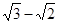
��1����E�A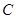 �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2����ֱ��(xi��n)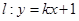 ���E�A
���E�A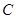 ��
��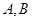 ���c(di��n)����(d��ng)
���c(di��n)����(d��ng)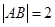 �r(sh��)��ֱ��(xi��n)
�r(sh��)��ֱ��(xi��n)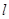 �ķ���
�ķ���
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
��֪�E�AC�����ҽ��c(di��n)����(bi��o)�քe��(- ,0),(
,0),( ,0),�x������
,0),�x������ .ֱ��(xi��n)y=t�c�E�AC���ڲ�ͬ�ă��c(di��n)M,N,�Ծ�(xi��n)��MN��ֱ�����AP,�A�Ğ�P.
.ֱ��(xi��n)y=t�c�E�AC���ڲ�ͬ�ă��c(di��n)M,N,�Ծ�(xi��n)��MN��ֱ�����AP,�A�Ğ�P.
(1)��E�AC�ķ���;
(2)��AP�cx�S����,��A��P������(bi��o);
(3)�O(sh��)Q(x,y)�LjAP�ϵĄ�(d��ng)�c(di��n),��(d��ng)t׃���r(sh��),��y�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�E�AE: +
+ =1(a>b>0)�����ҽ��c(di��n)�քe��F1,F2,������2,�^(gu��)F1����ֱ�ڙE�A�L(zh��ng)�S����PQ,|PQ|��3.
=1(a>b>0)�����ҽ��c(di��n)�քe��F1,F2,������2,�^(gu��)F1����ֱ�ڙE�A�L(zh��ng)�S����PQ,|PQ|��3.
(1)��E�AE�ķ���;
(2)���^(gu��)F1��ֱ��(xi��n)l���E�A��A,B���c(di��n),�Д��Ƿ����ֱ��(xi��n)lʹ�á�AF2B���g��,������,���l��б��k��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�O(sh��)�E�AC: +
+ =1(a>b>0)�^(gu��)�c(di��n)(0,4),�x���ʞ�
=1(a>b>0)�^(gu��)�c(di��n)(0,4),�x���ʞ� .
.
(1)��C�ķ���;
(2)���^(gu��)�c(di��n)(3,0)��б�ʞ� ��ֱ��(xi��n)��C���ؾ�(xi��n)�ε����c(di��n)����(bi��o).
��ֱ��(xi��n)��C���ؾ�(xi��n)�ε����c(di��n)����(bi��o).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�E�AC1: +
+ =1(a>b>0)��������c(di��n)�քe��A,B,�c(di��n)P���p����(xi��n)C2:
=1(a>b>0)��������c(di��n)�քe��A,B,�c(di��n)P���p����(xi��n)C2: -
- =1�ڵ�һ���ރ�(n��i)�ĈD����һ�c(di��n),ֱ��(xi��n)AP,BP�c�E�AC1�քe����C,D�c(di��n),��S��ACD=S��PCD.
=1�ڵ�һ���ރ�(n��i)�ĈD����һ�c(di��n),ֱ��(xi��n)AP,BP�c�E�AC1�քe����C,D�c(di��n),��S��ACD=S��PCD.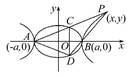
(1)��P�c(di��n)������(bi��o).
(2)�ܷ�ʹֱ��(xi��n)CD�^(gu��)�E�AC1���ҽ��c(di��n),����,����˕r(sh��)�p����(xi��n)C2���x����;������,Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com