
【題目】已知下列命題:
①命題“![]() ,
, ![]() ”的否定是:“
”的否定是:“![]() ,
, ![]() ”;
”;
②若樣本數(shù)據(jù)![]() 的平均值和方差分別為
的平均值和方差分別為![]() 和
和![]() 則數(shù)據(jù)
則數(shù)據(jù)![]() 的平均值和標(biāo)準(zhǔn)差分別為
的平均值和標(biāo)準(zhǔn)差分別為![]() ,
, ![]() ;
;
③兩個事件不是互斥事件的必要不充分條件是兩個事件不是對立事件;
④在![]() 列聯(lián)表中,若比值
列聯(lián)表中,若比值![]() 與
與![]() 相差越大,則兩個分類變量有關(guān)系的可能性就越大.
相差越大,則兩個分類變量有關(guān)系的可能性就越大.
⑤已知![]() 為兩個平面,且
為兩個平面,且![]() ,
, ![]() 為直線.則命題:“若
為直線.則命題:“若![]() ,則
,則![]() ”的逆命題和否命題均為假命題.
”的逆命題和否命題均為假命題.
⑥設(shè)定點![]() 、
、![]() ,動點
,動點![]() 滿足條件
滿足條件![]() 為正常數(shù)),則
為正常數(shù)),則![]() 的軌跡是橢圓.其中真命題的個數(shù)為( )
的軌跡是橢圓.其中真命題的個數(shù)為( )
A. 5 B. 4 C. 3 D. 2
【答案】A
【解析】①命題“![]() ,
, ![]() ”的否定是:“
”的否定是:“![]() ,
, ![]() ”,命題正確;
”,命題正確;
②數(shù)據(jù)![]() 的標(biāo)準(zhǔn)差
的標(biāo)準(zhǔn)差![]() ,平均數(shù)為:
,平均數(shù)為: ![]() ,
,
命題正確;
③其逆否命題是:兩事件是對立事件的必要不充分條件是兩個事件是互斥事件.命題正確;
④![]() ﹣
﹣![]() =
=![]() ,∵ad﹣bc相差越大,兩個分類變量有關(guān)系的可能性就越大,
,∵ad﹣bc相差越大,兩個分類變量有關(guān)系的可能性就越大,
∴![]() ﹣
﹣![]() =相差越大,兩個分類變量有關(guān)系的可能性就越大,命題正確;
=相差越大,兩個分類變量有關(guān)系的可能性就越大,命題正確;
⑤逆命題:已知![]() 為兩個平面,且
為兩個平面,且![]() ,
, ![]() 為直線.則命題:“若
為直線.則命題:“若![]() ,則
,則![]() ”顯然l與平面
”顯然l與平面![]() 關(guān)系不確定,所以逆命題為假命題,逆命題與否命題同真同假,故二者同為假命題;
關(guān)系不確定,所以逆命題為假命題,逆命題與否命題同真同假,故二者同為假命題;
⑥當(dāng)![]() 時,
時, ![]() 的軌跡是線段,顯然命題是假命題;
的軌跡是線段,顯然命題是假命題;
所以真命題個數(shù)為5個
故選:A


科目:高中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)《中華人民共和國道路交通安全法》規(guī)定:“車輛駕駛員血液酒精溶度(單位mg/100ml)/在![]() ,屬于酒后駕駛;血液濃度不低于80,屬于醉酒駕駛。”2017年“中秋節(jié)”晚9點開始,濟南市交警隊在桿石橋交通崗前設(shè)點,對過往的車輛進行檢查,經(jīng)過4個小時,共查處喝過酒的駕駛者60名,下圖是用酒精測試儀對這60名駕駛者血液中酒精溶度進行檢測后所得結(jié)果畫出的頻率分布直方圖。
,屬于酒后駕駛;血液濃度不低于80,屬于醉酒駕駛。”2017年“中秋節(jié)”晚9點開始,濟南市交警隊在桿石橋交通崗前設(shè)點,對過往的車輛進行檢查,經(jīng)過4個小時,共查處喝過酒的駕駛者60名,下圖是用酒精測試儀對這60名駕駛者血液中酒精溶度進行檢測后所得結(jié)果畫出的頻率分布直方圖。
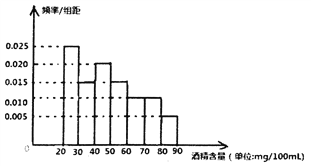
(1)求這60名駕駛者中屬于醉酒駕車的人數(shù)(圖中每組包括左端點,不包括右端點)
(2)若以各小組的中值為該組的估計值,頻率為概率的估計值,求這60名駕駛者血液的酒精濃度的平均值。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,以
中,以![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標(biāo)系,曲線
軸正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,
, ![]() 是曲線
是曲線![]() 與直線
與直線![]() :
: ![]() (
(![]() )的交點(異于原點
)的交點(異于原點![]() ).
).
(1)寫出![]() ,
, ![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)求過點![]() 和直線
和直線![]() 垂直的直線
垂直的直線![]() 的極坐標(biāo)方程.
的極坐標(biāo)方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知向量a=(2x-y+1,x+y-2),b=(2,-2).
①當(dāng)x、y為何值時,a與b共線?
②是否存在實數(shù)x、y,使得a⊥b,且|a|=|b|?若存在,求出xy的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() ,函數(shù)
,函數(shù)![]() 的圖像與函數(shù)
的圖像與函數(shù)![]() 的圖像相切,求
的圖像相切,求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,函數(shù)
,函數(shù)![]() 滿足對任意
滿足對任意![]() ,都有
,都有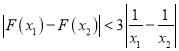 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)若![]() ,函數(shù)
,函數(shù)![]() ,且
,且![]() 有兩個極值點
有兩個極值點![]() ,其中
,其中![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() -
-![]() ,g(x)=
,g(x)= ![]() .
.
(1)若![]() ,函數(shù)
,函數(shù)![]() 的圖像與函數(shù)
的圖像與函數(shù)![]() 的圖像相切,求
的圖像相切,求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,函數(shù)
,函數(shù)![]() 滿足對任意
滿足對任意![]() (x1
(x1![]() x2),都有
x2),都有![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)若![]() ,函數(shù)
,函數(shù)![]() =f(x)+ g(x),且G(
=f(x)+ g(x),且G(![]() )有兩個極值點x1,x2,其中x1
)有兩個極值點x1,x2,其中x1![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的圖象在
的圖象在![]() 處的切線方程;
處的切線方程;
(2)若函數(shù)![]() 在定義域上為單調(diào)增函數(shù).
在定義域上為單調(diào)增函數(shù).
①求![]() 最大整數(shù)值;
最大整數(shù)值;
②證明: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩人進行射擊比賽,各射擊![]() 局,每局射擊
局,每局射擊![]() 次,射擊命中目標(biāo)得
次,射擊命中目標(biāo)得![]() 分,未命中目標(biāo)得
分,未命中目標(biāo)得![]() 分,兩人
分,兩人![]() 局的得分情況如下:
局的得分情況如下:
甲 |
|
|
|
|
乙 |
|
|
|
|
(Ⅰ)若從甲的![]() 局比賽中,隨機選取
局比賽中,隨機選取![]() 局,求這
局,求這![]() 局的得分恰好相等的概率.
局的得分恰好相等的概率.
(Ⅱ)如果![]() ,從甲、乙兩人的
,從甲、乙兩人的![]() 局比賽中隨機各選取
局比賽中隨機各選取![]() 局,記這
局,記這![]() 局的得分和為
局的得分和為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
(Ⅲ)在![]() 局比賽中,若甲、乙兩人的平均得分相同,且乙的發(fā)揮更穩(wěn)定,寫出
局比賽中,若甲、乙兩人的平均得分相同,且乙的發(fā)揮更穩(wěn)定,寫出![]() 的所有可能取值.(結(jié)論不要求證明)
的所有可能取值.(結(jié)論不要求證明)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com