
【題目】已知橢圓![]()
![]() 是橢圓內(nèi)任一點(diǎn).設(shè)經(jīng)過
是橢圓內(nèi)任一點(diǎn).設(shè)經(jīng)過![]() 的兩條不同直線
的兩條不同直線![]() 分別于橢圓交于點(diǎn)
分別于橢圓交于點(diǎn)![]() 記
記![]() 的斜率分別為
的斜率分別為![]()
(1)當(dāng)![]() 經(jīng)過橢圓右焦點(diǎn)且
經(jīng)過橢圓右焦點(diǎn)且![]() 為
為![]() 中點(diǎn)時(shí),求:
中點(diǎn)時(shí),求:
①橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
②四邊形![]() 面積
面積![]() 的取值范圍.
的取值范圍.
(2)當(dāng)![]() 時(shí),若點(diǎn)
時(shí),若點(diǎn)![]() 重合于點(diǎn)
重合于點(diǎn)![]()
![]() ,且
,且![]() .求證:直線
.求證:直線![]() 過定點(diǎn)
過定點(diǎn)![]() .
.
【答案】(1) ①![]() ;②
;②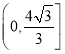 ;(2)見解析.
;(2)見解析.
【解析】
(1) ①由方程可求出焦點(diǎn)坐標(biāo),進(jìn)而可求![]() 的斜率.設(shè)出
的斜率.設(shè)出![]() ,將
,將![]() 代入到橢圓方程中去,將所得方程相減整理,
代入到橢圓方程中去,將所得方程相減整理, ![]() ,結(jié)合中點(diǎn)坐標(biāo)和
,結(jié)合中點(diǎn)坐標(biāo)和![]() 的斜率可求
的斜率可求![]() .
.
②由分析知, 當(dāng)過![]() 點(diǎn)與
點(diǎn)與![]() 的直線同時(shí)和橢圓相切時(shí)四邊形
的直線同時(shí)和橢圓相切時(shí)四邊形![]() 的面積最大. 設(shè)切線方程為
的面積最大. 設(shè)切線方程為![]() ,與橢圓聯(lián)立整理后令
,與橢圓聯(lián)立整理后令![]() ,即可求出切點(diǎn)
,即可求出切點(diǎn)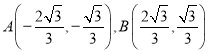 ,進(jìn)而可求切點(diǎn)到直線
,進(jìn)而可求切點(diǎn)到直線![]() 的距離
的距離![]() ,由弦長(zhǎng)公式求出
,由弦長(zhǎng)公式求出![]() 的長(zhǎng)度,進(jìn)而可求四邊形的面積.
的長(zhǎng)度,進(jìn)而可求四邊形的面積.
(2)設(shè)出![]() 的方程,與橢圓聯(lián)立,得到
的方程,與橢圓聯(lián)立,得到![]() 橫坐標(biāo)的關(guān)系,由
橫坐標(biāo)的關(guān)系,由![]() ,可求出
,可求出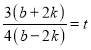 ,進(jìn)而可知
,進(jìn)而可知![]() .因此可證過定點(diǎn).
.因此可證過定點(diǎn).
(1) ①解:由題意知,![]() .即橢圓的焦點(diǎn)坐標(biāo)為
.即橢圓的焦點(diǎn)坐標(biāo)為![]() .
.
則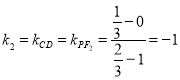 .設(shè)
.設(shè)![]()
則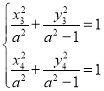 兩式相減整理得
兩式相減整理得![]()
![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),![]() 解得
解得![]()
故橢圓的方程為![]() .
.
②解:由題意知,當(dāng)過![]() 點(diǎn)與
點(diǎn)與![]() 的直線同時(shí)和橢圓相切時(shí)四邊形
的直線同時(shí)和橢圓相切時(shí)四邊形![]() 的面積最大.
的面積最大.
由![]() 知,切線斜率也為
知,切線斜率也為![]() .設(shè)切線方程為
.設(shè)切線方程為![]() ,與橢圓聯(lián)立得
,與橢圓聯(lián)立得
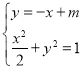 ,整理得
,整理得![]() ,則
,則
![]() ,解得
,解得![]() .
.
則可求切點(diǎn)不妨設(shè)為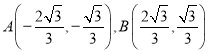 ,此時(shí)兩點(diǎn)到
,此時(shí)兩點(diǎn)到![]() 的距離
的距離
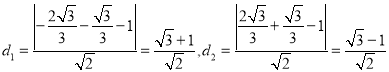
設(shè)![]() ,聯(lián)立
,聯(lián)立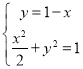 ,整理得
,整理得![]() ,則
,則
由韋達(dá)定理知![]() .
.
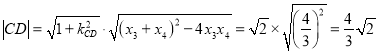
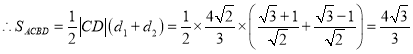
故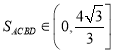 .
.
(2)證明:當(dāng)![]() 時(shí),橢圓的方程為
時(shí),橢圓的方程為![]() .
.
![]()
![]() 直線
直線![]() 的斜率存在且不為0,直線
的斜率存在且不為0,直線![]() 不過
不過![]()
設(shè)直線![]() 的方程為
的方程為![]() ,
,![]() 此時(shí)
此時(shí)![]()
聯(lián)立得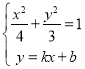 ,整理得
,整理得![]()
則![]() .
.![]()

即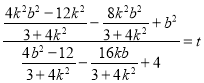 整理得
整理得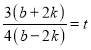
解得![]() 此時(shí)
此時(shí)![]()
故直線![]() 恒過
恒過![]() .
.


 導(dǎo)學(xué)全程練創(chuàng)優(yōu)訓(xùn)練系列答案
導(dǎo)學(xué)全程練創(chuàng)優(yōu)訓(xùn)練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知f(x)=|2x+4|+|x-3|.
(1)解關(guān)于x的不等式f(x)<8;
(2)對(duì)于正實(shí)數(shù)a,b,函數(shù)g(x)=f(x)-3a-4b只有一個(gè)零點(diǎn),求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】
設(shè)函數(shù)![]()
(Ⅰ)若![]() 是函數(shù)
是函數(shù)![]() 的極值點(diǎn),1和
的極值點(diǎn),1和![]() 是
是![]() 的兩個(gè)不同零點(diǎn),且
的兩個(gè)不同零點(diǎn),且![]()
且![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若對(duì)任意![]() , 都存在
, 都存在![]() (
(![]() 為自然對(duì)數(shù)的底數(shù)),使得
為自然對(duì)數(shù)的底數(shù)),使得![]()
成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為直角梯形,
為直角梯形,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).
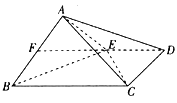
(Ⅰ)證明:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)若![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】近幾年,我國(guó)鮮切花產(chǎn)業(yè)得到了快速發(fā)展,相關(guān)部門制定了鮮切花產(chǎn)品行業(yè)等級(jí)標(biāo)準(zhǔn),統(tǒng)一使用綜合指標(biāo)值![]() 進(jìn)行衡量,如下表所示.某花卉生產(chǎn)基地準(zhǔn)備購進(jìn)一套新型的生產(chǎn)線,現(xiàn)進(jìn)行設(shè)備試用,分別從新舊兩條生產(chǎn)線加工的產(chǎn)品中選取30個(gè)樣品進(jìn)行等級(jí)評(píng)定,整理成如圖所示的莖葉圖.
進(jìn)行衡量,如下表所示.某花卉生產(chǎn)基地準(zhǔn)備購進(jìn)一套新型的生產(chǎn)線,現(xiàn)進(jìn)行設(shè)備試用,分別從新舊兩條生產(chǎn)線加工的產(chǎn)品中選取30個(gè)樣品進(jìn)行等級(jí)評(píng)定,整理成如圖所示的莖葉圖.
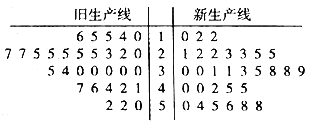
綜合指標(biāo) |
|
|
|
質(zhì)量等級(jí) | 三級(jí) | 二級(jí) | 一級(jí) |
(Ⅰ)根據(jù)莖葉圖比較兩條生產(chǎn)線加工的產(chǎn)品的綜合指標(biāo)值的平均值及分散程度(直接給出結(jié)論即可);
(Ⅱ)若從等級(jí)為三級(jí)的樣品中隨機(jī)選取3個(gè)進(jìn)行生產(chǎn)流程調(diào)查,其中來自新型生產(chǎn)線的樣品個(gè)數(shù)為![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)根據(jù)該花卉生產(chǎn)基地的生產(chǎn)記錄,原有生產(chǎn)線加工的產(chǎn)品的單件平均利潤(rùn)為4元,產(chǎn)品的銷售率(某等級(jí)產(chǎn)品的銷量與產(chǎn)量的比值)及產(chǎn)品售價(jià)如下表:
三級(jí)花 | 二級(jí)花 | 一級(jí)花 | |
銷售率 |
|
|
|
單件售價(jià) | 12元 | 16元 | 20元 |
預(yù)計(jì)該新型生產(chǎn)線加工的鮮切花單件產(chǎn)品的成本為span>10元,日產(chǎn)量3000件.因?yàn)轷r切花產(chǎn)品的保鮮特點(diǎn),未售出的產(chǎn)品統(tǒng)一按原售價(jià)的50%全部處理完.如果僅從單件產(chǎn)品利潤(rùn)的角度考慮,該生產(chǎn)基地是否需要引進(jìn)該新型生產(chǎn)線?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩位同學(xué)參加某個(gè)知識(shí)答題游戲節(jié)目,答題分兩輪,第一輪為“選題答題環(huán)節(jié)”第二輪為“輪流坐莊答題環(huán)節(jié)”.首先進(jìn)行第一輪“選題答題環(huán)節(jié)”,答題規(guī)則是:每位同學(xué)各自從備選的5道不同題中隨機(jī)抽出3道題進(jìn)行答題,答對(duì)一題加10分,答錯(cuò)一題(不答視為答錯(cuò))減5分,已知甲能答對(duì)備選5道題中的每道題的概率都是![]() ,乙恰能答對(duì)備選5道題中的其中3道題;第一輪答題完畢后進(jìn)行第二輪“輪流坐莊答題環(huán)節(jié)”,答題規(guī)則是:先確定一人坐莊答題,若答對(duì),繼續(xù)答下一題…,直到答錯(cuò),則換人(換莊)答下一題…以此類推.例如若甲首先坐莊,則他答第1題,若答對(duì)繼續(xù)答第2題,如果第2題也答對(duì),繼續(xù)答第3題,直到他答錯(cuò)則換成乙坐莊開始答下一題,…直到乙答錯(cuò)再換成甲坐莊答題,依次類推兩人共計(jì)答完20道題游戲結(jié)束,假設(shè)由第一輪答題得分期望高的同學(xué)在第二輪環(huán)節(jié)中最先開始作答,且記第
,乙恰能答對(duì)備選5道題中的其中3道題;第一輪答題完畢后進(jìn)行第二輪“輪流坐莊答題環(huán)節(jié)”,答題規(guī)則是:先確定一人坐莊答題,若答對(duì),繼續(xù)答下一題…,直到答錯(cuò),則換人(換莊)答下一題…以此類推.例如若甲首先坐莊,則他答第1題,若答對(duì)繼續(xù)答第2題,如果第2題也答對(duì),繼續(xù)答第3題,直到他答錯(cuò)則換成乙坐莊開始答下一題,…直到乙答錯(cuò)再換成甲坐莊答題,依次類推兩人共計(jì)答完20道題游戲結(jié)束,假設(shè)由第一輪答題得分期望高的同學(xué)在第二輪環(huán)節(jié)中最先開始作答,且記第![]() 道題也由該同學(xué)(最先答題的同學(xué))作答的概率為
道題也由該同學(xué)(最先答題的同學(xué))作答的概率為![]() (
(![]() ),其中
),其中![]() ,已知供甲乙回答的20道題中,甲,乙兩人答對(duì)其中每道題的概率都是
,已知供甲乙回答的20道題中,甲,乙兩人答對(duì)其中每道題的概率都是![]() ,如果某位同學(xué)有機(jī)會(huì)答第
,如果某位同學(xué)有機(jī)會(huì)答第![]() 道題且回答正確則該同學(xué)加10分,答錯(cuò)(不答視為答錯(cuò))則減5分,甲乙答題相互獨(dú)立;兩輪答題完畢總得分高者勝出.回答下列問題
道題且回答正確則該同學(xué)加10分,答錯(cuò)(不答視為答錯(cuò))則減5分,甲乙答題相互獨(dú)立;兩輪答題完畢總得分高者勝出.回答下列問題
(1)請(qǐng)預(yù)測(cè)第二輪最先開始作答的是誰?并說明理由
(2)①求第二輪答題中![]() ,
,![]() ;
;
②求證![]() 為等比數(shù)列,并求
為等比數(shù)列,并求![]() (
(![]() )的表達(dá)式.
)的表達(dá)式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)當(dāng)![]() 時(shí),關(guān)于
時(shí),關(guān)于![]() 的方程
的方程![]() 有兩個(gè)不同的實(shí)數(shù)解
有兩個(gè)不同的實(shí)數(shù)解![]() ,
,![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (m
(m![]() R)的導(dǎo)函數(shù)為
R)的導(dǎo)函數(shù)為![]() .
.
(1)若函數(shù)![]() 存在極值,求m的取值范圍;
存在極值,求m的取值范圍;
(2)設(shè)函數(shù)![]() (其中e為自然對(duì)數(shù)的底數(shù)),對(duì)任意m
(其中e為自然對(duì)數(shù)的底數(shù)),對(duì)任意m![]() R,若關(guān)于x的不等式
R,若關(guān)于x的不等式![]() 在(0,
在(0,![]() )上恒成立,求正整數(shù)k的取值集合.
)上恒成立,求正整數(shù)k的取值集合.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,已知PA⊥平面ABCD,且四邊形ABCD為直角梯形,∠ABC=∠BAD=![]() ,PA=AD=2,AB=BC=1,點(diǎn)M、E分別是PA、PD的中點(diǎn)
,PA=AD=2,AB=BC=1,點(diǎn)M、E分別是PA、PD的中點(diǎn)
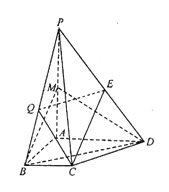
(1)求證:CE//平面BMD
(2)點(diǎn)Q為線段BP中點(diǎn),求直線PA與平面CEQ所成角的余弦值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com