已知數列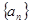
滿足
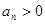且對一切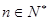
,
有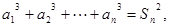
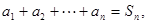
（Ⅰ）求證：對一切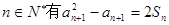
（Ⅱ）求數列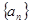通項公式.
（Ⅲ）求證：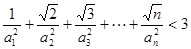
【解析】第一問利用，已知表達式，可以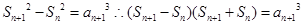得到
，然后得到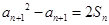
，從而求證
。
第二問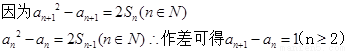
，可得數列的通項公式。
第三問中，利用放縮法的思想，我們可以得到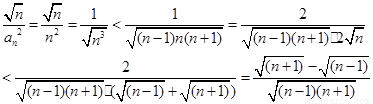
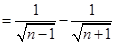然后利用累加法思想求證得到證明。
解: (1) 證明:
名師指導期末沖刺卷系列答案科目：高中數學 來源： 題型：
| b1 |
| a1 |
| b2 |
| 2a2 |
| bn |
| nan |
查看答案和解析>>
科目：高中數學 來源：2010年河南省鶴壁市高二下學期第一次段考數學試題 題型：解答題
已知數列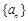
滿足
且
(1) 證明：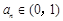
；
(2) 比較an與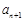
的大小；
(3) 是否存在正實數c，使得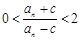
，對一切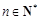
恒成立？若存在，則求出c的取值范圍；若不存在，說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
滿足
,且對一切
,有
,其中
.
的通項公式； (Ⅱ)求證：
.
滿足
,且對一切
有
,其中
, 
，并求數列
，求數列
的前
項和
;
.