
【題目】在平面直角坐標(biāo)系中,設(shè)![]() 為不同的兩點(diǎn),直線
為不同的兩點(diǎn),直線![]() 的方程為
的方程為![]() ,設(shè)
,設(shè)![]() ,其中
,其中![]() 均為實(shí)數(shù).下列四個說法中:
均為實(shí)數(shù).下列四個說法中:
①存在實(shí)數(shù)![]() ,使點(diǎn)
,使點(diǎn)![]() 在直線
在直線![]() 上;
上;
②若![]() ,則過
,則過![]() 兩點(diǎn)的直線與直線
兩點(diǎn)的直線與直線![]() 重合;
重合;
③若![]() ,則直線
,則直線![]() 經(jīng)過線段
經(jīng)過線段![]() 的中點(diǎn);
的中點(diǎn);
④若![]() ,則點(diǎn)
,則點(diǎn)![]() 在直線
在直線![]() 的同側(cè),且直線
的同側(cè),且直線![]() 與線段
與線段![]() 的延長線相交.
的延長線相交.
所有結(jié)論正確的說法的序號是______________.
【答案】③④
【解析】
①點(diǎn)在直線上,則點(diǎn)的坐標(biāo)滿足直線方程,從而得到ax2+bx2+c=0,進(jìn)而可判斷①不正確;
②若δ=1,則ax1+by1+c=ax2+by2+c,進(jìn)而得到![]() ,根據(jù)兩直線斜率的關(guān)系即可判定過M、N兩點(diǎn)的直線與直線l平行或重合;
,根據(jù)兩直線斜率的關(guān)系即可判定過M、N兩點(diǎn)的直線與直線l平行或重合;
③若δ=﹣1,則ax1+by1+c+ax2+by2+c=0,從而得到即![]() ,所以直線l經(jīng)過線段MN的中點(diǎn);
,所以直線l經(jīng)過線段MN的中點(diǎn);
④若δ>1,則ax1+by1+c>ax2+by2+c>0,或ax1+by2+c<ax2+by2+c<0,根據(jù)點(diǎn)與直線的位置關(guān)系可知點(diǎn)M,N在直線l同側(cè),從而可判定④正確.
若點(diǎn)N在直線l上則ax2+bx2+c=0,
∴不存在實(shí)數(shù)δ,使點(diǎn)N在直線l上,
故①不正確;
若δ=1,則ax1+by1+c=ax2+by2+c,
即![]() ,
,
∴kMN=kl,
即過M、N兩點(diǎn)的直線與直線l平行或重合,
故②錯誤;
若δ=﹣1,則ax1+by1+c+ax2+by2+c=0
即,![]() ,
,
∴直線l經(jīng)過線段MN的中點(diǎn),
即③正確;
若δ>1,則ax1+by1+c>ax2+by2+c>0,
或ax1+by2+c<ax2+by2+c<0,
即點(diǎn)M、N在直線l的同側(cè),且直線l與線段MN不平行.
故④正確.
故答案為:③④.


 新編小學(xué)單元自測題系列答案
新編小學(xué)單元自測題系列答案 字詞句段篇系列答案
字詞句段篇系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在Rt△ABC中,AC⊥BC,過點(diǎn)C的直線VC垂直于平面ABC,D、E分別為線段VA、VC上異于端點(diǎn)的點(diǎn). 
(1)當(dāng)DE⊥平面VBC時,判斷直線DE與平面ABC的位置關(guān)系,并說明理由;
(2)當(dāng)D、E、F分別為線段VA、VC、AB上的中點(diǎn),且VC=2BC時,求二面角B﹣DE﹣F的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
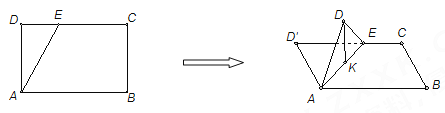
【題目】如圖,在長方形![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 為線段
為線段![]() 上一動點(diǎn),現(xiàn)將
上一動點(diǎn),現(xiàn)將![]() 沿
沿![]() 折起,使點(diǎn)
折起,使點(diǎn)![]() 在面
在面![]() 內(nèi)的射影
內(nèi)的射影![]() 在直線
在直線![]() 上,當(dāng)點(diǎn)
上,當(dāng)點(diǎn)![]() 從
從![]() 運(yùn)動到
運(yùn)動到![]() ,則點(diǎn)
,則點(diǎn)![]() 所形成軌跡的長度為( )
所形成軌跡的長度為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】云南省2016年高中數(shù)學(xué)學(xué)業(yè)水平考試的原始成績采用百分制,發(fā)布成績使用等級制,各登記劃分標(biāo)準(zhǔn)為:85分及以上,記為A等,分?jǐn)?shù)在[70,85)內(nèi),記為B等,分?jǐn)?shù)在[60,70)內(nèi),記為C等,60分以下,記為D等,同時認(rèn)定等級分別為A,B,C都為合格,等級為D為不合格. 已知甲、乙兩所學(xué)校學(xué)生的原始成績均分布在[50,100]內(nèi),為了比較兩校學(xué)生的成績,分別抽取50名學(xué)生的原始成績作為樣本進(jìn)行統(tǒng)計,按照[50,60),[60,70),[70,80),[80,90),[90,100]分別作出甲校如圖1所示樣本頻率分布直方圖,乙校如圖2所示樣本中等級為C、D的所有數(shù)據(jù)莖葉圖.
(1)求圖中x的值,并根據(jù)樣本數(shù)據(jù)比較甲乙兩校的合格率;
(2)在選取的樣本中,從甲、乙兩校C等級的學(xué)生中隨機(jī)抽取3名學(xué)生進(jìn)行調(diào)研,用X表示所抽取的3名學(xué)生中甲校的學(xué)生人數(shù),求隨機(jī)變量X的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓 ![]() 的右焦點(diǎn)為F,設(shè)直線l:x=5與x軸的交點(diǎn)為E,過點(diǎn)F且斜率為k的直線l1與橢圓交于A,B兩點(diǎn),M為線段EF的中點(diǎn).
的右焦點(diǎn)為F,設(shè)直線l:x=5與x軸的交點(diǎn)為E,過點(diǎn)F且斜率為k的直線l1與橢圓交于A,B兩點(diǎn),M為線段EF的中點(diǎn).
(I)若直線l1的傾斜角為 ![]() ,求△ABM的面積S的值;
,求△ABM的面積S的值;
(Ⅱ)過點(diǎn)B作直線BN⊥l于點(diǎn)N,證明:A,M,N三點(diǎn)共線.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)各項均為正數(shù)的數(shù)列{an}的前n項和為Sn , 且滿足2 ![]() =an+1(n∈N*).
=an+1(n∈N*).
(Ⅰ)求數(shù)列{an}的通項公式;
(Ⅱ)若bn=(an+1)2 ![]() ,求數(shù)列{bn}的前n項和Tn .
,求數(shù)列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】執(zhí)行如圖所示的程序框圖,若輸入a,b,c分別為1,2,0.3,則輸出的結(jié)果為( ) 
A.1.125
B.1.25
C.1.3125
D.1.375
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,三棱柱ABC﹣DEF中,側(cè)面ABED是邊長為2的菱形,且∠ABE= ![]() ,BC=
,BC= ![]() ,四棱錐F﹣ABED的體積為2,點(diǎn)F在平面ABED內(nèi)的正投影為G,且G在AE上,點(diǎn)M是在線段CF上,且CM=
,四棱錐F﹣ABED的體積為2,點(diǎn)F在平面ABED內(nèi)的正投影為G,且G在AE上,點(diǎn)M是在線段CF上,且CM= ![]() CF.
CF.
(Ⅰ)證明:直線GM∥平面DEF;
(Ⅱ)求二面角M﹣AB﹣F的余弦值.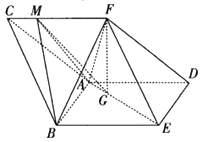
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com