【題目】某商場舉行元旦促銷回饋活動，凡購物滿1000元，即可參與抽獎活動，抽獎規則如下：在一個不透明的口袋中裝有編號為1、2、3、4、5的5個完全相同的小球，顧客每次從口袋中摸出一個小球，共摸三次（每次摸出的小球均不放回口袋），編號依次作為一個三位數的個位、十位、百位，若三位數是奇數，則獎勵50元，若三位數是偶數，則獎勵
元（
為三位數的百位上的數字，如三位數為234，則獎勵
元）.
（1）求抽獎者在一次抽獎中所得三位數是奇數的概率；
（2）求抽獎者在一次抽獎中獲獎金額
的概率分布與期望
.
【答案】（1）
（2）見解析，期望是150元.
【解析】
（1）首先利用排列求出摸三次的總的基本事件個數：
；然后利用分步計數原理求出個位的排法、十位百位的排法求出三位數是奇數的基本事件個數，再利用古典概型的概率計算公式即可求解.
（2）獲獎金額
的可能取值為50、100、200、300、400、500，求出各個隨機變量的分布列，利用均值公式即可求解.
解：（1）因為總的基本事件個數，摸到三位數是奇數的事件數
，所以
；
所以摸到三位數是奇數的概率.
（2）獲獎金額的可能取值為50、100、200、300、400、500，
，
，
，
，
，
，
獲獎金額的概率分布為
| 50 | 100 | 200 | 300 | 400 | 500 |
|
|
|
|
|
|
|
均值
元.
所以期望是150元.
七彩題卡口算應用一點通系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）＝axlnx﹣x2﹣ax+1（a∈R）在定義域內有兩個不同的極值點.
（1）求實數a的取值范圍；
（2）設兩個極值點分別為x1，x2，x1＜x2，證明：f（x1）+f（x2）＜2﹣x12+x22.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知平面
平面ABC，P、P在平面ABC的同側，二面角
的平面角為鈍角，Q到平面ABC的距離為
，
是邊長為2的正三角形，
，
，
.
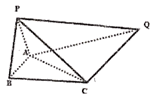
（1）求證：面
平面PAB；
（2）求二面角
的平面角的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C：
（
）的離心率為
，點
在橢圓C上，直線
與橢圓C交于不同的兩點A，B.
（1）求橢圓C的方程；
（2）直線
，
分別交y軸于M，N兩點，問：x軸上是否存在點Q，使得
？若存在，求出點Q的坐標；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了實施“科技下鄉，精準脫貧”戰略，某縣科技特派員帶著
，
，
三個農業扶貧項目進駐某村，對該村僅有的甲、乙、丙、丁四個貧困戶進行產業幫扶．經過前期實際調研得知，這四個貧困戶選擇，，三個扶貧項目的意向如下表：
扶貧項目 |
|
|
|
貧困戶 | 甲、乙、丙、丁 | 甲、乙、丙 | 丙、丁 |
若每個貧困戶只能從自己已登記的選擇意向項目中隨機選取一項，且每個項目至多有兩個貧困戶選擇，則不同的選法種數有（ ）
A.24種B.16種C.10種D.8種
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，曲線
：
（
為參數），以坐標原點為極點，以
軸的正半軸為極軸，建立極坐標系，曲線
：
.
（1）寫出曲線的普通方程和曲線的直角坐標方程；
（2）若曲線上有一動點
，曲線上有一動點
，求
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
