
【題目】已知橢圓C1的方程為![]() ,雙曲線C2的左、右焦點(diǎn)分別是C1的左、右頂點(diǎn),而C2的左、右頂點(diǎn)分別是C1的左、右焦點(diǎn),O為坐標(biāo)原點(diǎn).
,雙曲線C2的左、右焦點(diǎn)分別是C1的左、右頂點(diǎn),而C2的左、右頂點(diǎn)分別是C1的左、右焦點(diǎn),O為坐標(biāo)原點(diǎn).
(1)求雙曲線C2的方程;
(2)若直線l:y=kx+![]() 與雙曲線C2恒有兩個(gè)不同的交點(diǎn)A和B,且
與雙曲線C2恒有兩個(gè)不同的交點(diǎn)A和B,且![]() ,求k的取值范圍.
,求k的取值范圍.
【答案】(1)![]() ;(2)
;(2)
【解析】試題分析:(1)由兩曲線長軸與焦點(diǎn)關(guān)系,求出雙曲線C2的方程。(2)設(shè)A(x1,y1),B(x2,y2),直線與雙曲線組方程組,得到韋達(dá)定理關(guān)系,注意判別式控制參數(shù)k范圍。把向量關(guān)系![]() >2,坐標(biāo)化即x1x2+y1y2>2,代入韋達(dá)可求。
>2,坐標(biāo)化即x1x2+y1y2>2,代入韋達(dá)可求。
試題解析:(1)設(shè)雙曲線C2的方程為![]()
則a2=4-1=3,c2=4,再由a2+b2=c2,得b2=1,
故雙曲線C2的方程為![]() -y2=1.
-y2=1.
(2)將y=kx+![]() 代入
代入![]() -y2=1,
-y2=1,
得(1-3k2)x2-6![]() kx-9=0.
kx-9=0.
由直線l與雙曲線C2交于不同的兩點(diǎn),
得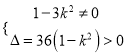
∴k2<1且k2≠![]() .①
.①
設(shè)A(x1,y1),B(x2,y2),
則x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
∴x1x2+y1y2=x1x2+(kx1+![]() )(kx2+
)(kx2+![]() )
)
=(k2+1)x1x2+![]() k(x1+x2)+2=
k(x1+x2)+2=![]() .
.
又∵![]() >2,即x1x2+y1y2>2,∴
>2,即x1x2+y1y2>2,∴![]() >2 >2,即
>2 >2,即![]() >0,
>0,
解得![]() <k2<3.②
<k2<3.②
由①②得![]() <k2<1,
<k2<1,
故k的取值范圍為



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分12分)
某企業(yè)生產(chǎn)A,B兩種產(chǎn)品,根據(jù)市場調(diào)查與預(yù)測,A產(chǎn)品的利潤與投資成正比,其關(guān)系如圖1;B產(chǎn)品的利潤與投資的算術(shù)平方根成正比,其關(guān)系如圖2(注:利潤和投資單位:萬元).

(1)分別將A、B兩種產(chǎn)品的利潤表示為投資的函數(shù)關(guān)系式;
(2)已知該企業(yè)已籌集到18萬元資金,并將全部投入A,B兩種產(chǎn)品的生產(chǎn).
①若平均投入生產(chǎn)兩種產(chǎn)品,可獲得多少利潤?
②問:如果你是廠長,怎樣分配這18萬元投資,才能使該企業(yè)獲得最大利潤?其最大利潤約為多少萬元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求
時(shí),求![]() 在區(qū)間
在區(qū)間![]() 上的最大值和最小值;
上的最大值和最小值;
(2)若對(duì)![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,近日我漁船編隊(duì)在島![]() 周圍海域作業(yè),在島
周圍海域作業(yè),在島![]() 的南偏西20°方向有一個(gè)海面觀測站
的南偏西20°方向有一個(gè)海面觀測站![]() ,某時(shí)刻觀測站發(fā)現(xiàn)有不明船只向我漁船編隊(duì)靠近,現(xiàn)測得與
,某時(shí)刻觀測站發(fā)現(xiàn)有不明船只向我漁船編隊(duì)靠近,現(xiàn)測得與![]() 相距31海里的
相距31海里的![]() 處有一艘海警船巡航,上級(jí)指示海警船沿北偏西40°方向,以40海里/小時(shí)的速度向島
處有一艘海警船巡航,上級(jí)指示海警船沿北偏西40°方向,以40海里/小時(shí)的速度向島![]() 直線航行以保護(hù)我漁船編隊(duì),30分鐘后到達(dá)
直線航行以保護(hù)我漁船編隊(duì),30分鐘后到達(dá)![]() 處,此時(shí)觀測站測得
處,此時(shí)觀測站測得![]() 間的距離為21海里.
間的距離為21海里.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)試問海警船再向前航行多少分鐘方可到島![]() ?
?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=cosx(acosx﹣sinx)![]() (a∈R),且f (
(a∈R),且f (![]() )
)![]() .
.
(1)求a的值;
(2)求f(x)的單調(diào)遞增區(qū)間;
(3)求f(x)在區(qū)間[0,![]() ]上的最小值及對(duì)應(yīng)的x的值.
]上的最小值及對(duì)應(yīng)的x的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地棚戶區(qū)改造建筑平面示意圖如圖所示,經(jīng)規(guī)劃調(diào)研確定,棚改規(guī)劃建筑用地區(qū)域近似為圓面,該圓面的內(nèi)接四邊形![]() 是原棚戶區(qū)建筑用地,測量可知邊界
是原棚戶區(qū)建筑用地,測量可知邊界![]() 萬米,
萬米,![]() 萬米,
萬米,![]() 萬米.
萬米.
(1)請(qǐng)計(jì)算原棚戶區(qū)建筑用地![]() 的面積及
的面積及![]() 的長;
的長;
(2)因地理?xiàng)l件的限制,邊界![]() 不能更改,而邊界
不能更改,而邊界![]() 可以調(diào)整,為了提高棚戶區(qū)建筑用地的利用率,請(qǐng)?jiān)趫A弧
可以調(diào)整,為了提高棚戶區(qū)建筑用地的利用率,請(qǐng)?jiān)趫A弧![]() 上設(shè)計(jì)一點(diǎn)
上設(shè)計(jì)一點(diǎn)![]() ,使得棚戶區(qū)改造后的新建筑用地
,使得棚戶區(qū)改造后的新建筑用地![]() 的面積最大,并求出最大值.
的面積最大,并求出最大值.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
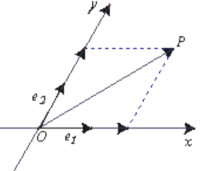
【題目】如圖,設(shè)![]() 是平面內(nèi)相交成
是平面內(nèi)相交成![]() 角的兩條數(shù)軸 ,
角的兩條數(shù)軸 ,![]() 分別是
分別是![]() 軸,
軸,![]() 軸正方向同向的單位向量,若向量
軸正方向同向的單位向量,若向量![]() ,則把有序數(shù)對(duì)
,則把有序數(shù)對(duì)![]() 叫做向量
叫做向量![]() 在坐標(biāo)系
在坐標(biāo)系![]() 中的坐標(biāo),假設(shè)
中的坐標(biāo),假設(shè)![]() .
.
(1)計(jì)算![]() 的大小;
的大小;
(2)設(shè)向量![]() ,若
,若![]() 與
與![]() 共線,求實(shí)數(shù)
共線,求實(shí)數(shù)![]() 的值;
的值;
(3)是否存在實(shí)數(shù)![]() ,使得
,使得![]() 與向量
與向量![]() 垂直,若存在求出
垂直,若存在求出![]() 的值,若不存在請(qǐng)說明理由.
的值,若不存在請(qǐng)說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】從甲地到乙地沿某條公路行駛一共200公里,遇到紅燈個(gè)數(shù)的概率如下表所示:
紅燈個(gè)數(shù) | 0 | 1 | 2 | 3 | 4 | 5 | 6個(gè)及6個(gè)以上 |
概率 | 0.02 | 0.1 |
| 0.35 | 0.2 | 0.1 | 0.03 |
(1)求表中字母![]() 的值;
的值;
(2)求至少遇到4個(gè)紅燈的概率;
(3)求至多遇到5個(gè)紅燈的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的單調(diào)區(qū)間;
(Ⅱ)已知f(x)在x=1處取得極大值.求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com