
【題目】定義:在數列![]() 中,若
中,若![]() 為常數)則稱
為常數)則稱![]() 為“等方差數列”,下列是對“等方差數列”的有關判斷( )
為“等方差數列”,下列是對“等方差數列”的有關判斷( )
①若![]() 是“等方差數列”,在數列
是“等方差數列”,在數列![]() 是等差數列;
是等差數列;
②![]() 是“等方差數列”;
是“等方差數列”;
③若![]() 是“等方差數列”,則數列
是“等方差數列”,則數列![]() 為常)也是“等方差數列”;
為常)也是“等方差數列”;
④若![]() 既是“等方差數列”又是等差數列,則該數列是常數數列.
既是“等方差數列”又是等差數列,則該數列是常數數列.
其中正確命題的個數為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中數學 來源: 題型:
【題目】設函數![]() .
.
(1)函數![]() 在區間
在區間![]() 是單調函數,求實數
是單調函數,求實數![]() 的取值范圍;
的取值范圍;
(2)若存在![]() ,使得
,使得![]() 成立,求滿足條件的最大整數
成立,求滿足條件的最大整數![]() ;
;
(3)如果對任意的![]() 都有
都有![]() 成立,求實數
成立,求實數![]() 的范圍.
的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空間四邊形PABC的各邊及對角線長度都相等,D、E、F、G分別是AB、BC、CA、AP的中點,下列四個結論中成立的是
①BC∥平面PDF
②DF⊥平面PAE
③平面GDF∥平面PBC
④平面PAE⊥平面ABC.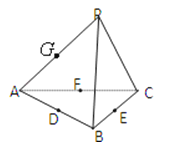
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩定點![]() ,
, ![]() 和一動點
和一動點![]() ,給出下列結論:
,給出下列結論:
①若![]() ,則點
,則點![]() 的軌跡是橢圓;
的軌跡是橢圓;
②若![]() ,則點
,則點![]() 的軌跡是雙曲線;
的軌跡是雙曲線;
③若![]() ,則點
,則點![]() 的軌跡是圓;
的軌跡是圓;
④若![]() ,則點
,則點![]() 的軌跡關于原點對稱;
的軌跡關于原點對稱;
⑤若直線![]() 與
與![]() 斜率之積等于
斜率之積等于![]() ,則點
,則點![]() 的軌跡是橢圓(除長軸兩端點).
的軌跡是橢圓(除長軸兩端點).
其中正確的是__________(填序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某科研小組研究發現:一棵水蜜桃樹的產量![]() (單位:百千克)與肥料費用
(單位:百千克)與肥料費用![]() (單位:百元)滿足如下關系:
(單位:百元)滿足如下關系:![]() ,且投入的肥料費用不超過5百元.此外,還需要投入其他成本(如施肥的人工費等)
,且投入的肥料費用不超過5百元.此外,還需要投入其他成本(如施肥的人工費等)![]() 百元.已知這種水蜜桃的市場售價為16元/千克(即16百元/百千克),且市場需求始終供不應求.記該棵水蜜桃樹獲得的利潤為
百元.已知這種水蜜桃的市場售價為16元/千克(即16百元/百千克),且市場需求始終供不應求.記該棵水蜜桃樹獲得的利潤為![]() (單位:百元).
(單位:百元).
(1)求利潤函數![]() 的函數關系式,并寫出定義域;
的函數關系式,并寫出定義域;
(2)當投入的肥料費用為多少時,該水蜜桃樹獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】判斷下列命題的真假,并說明理由.
(1)x∈R,都有x2-x+1>![]() ;
;
(2)α,β,使cos(α-β)=cos α-cos β;
(3)x,y∈N,都有(x-y)∈N;
(4)x,y∈Z,使![]() x+y=3.
x+y=3.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 在實數集
在實數集![]() 上的圖象是連續不斷的,且對任意實數
上的圖象是連續不斷的,且對任意實數![]() 存在常數
存在常數![]() 使得
使得![]() 恒成立,則稱
恒成立,則稱![]() 是一個“關于
是一個“關于![]() 函數”.現有下列“關于
函數”.現有下列“關于![]() 函數”的結論:
函數”的結論:
①常數函數是“關于![]() 函數”;
函數”;
②正比例函數必是一個“關于![]() 函數”;
函數”;
③“關于![]() 函數”至少有一個零點;
函數”至少有一個零點;
④![]() 是一個“關于
是一個“關于![]() 函數”.
函數”.
其中正確結論的序號是_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系下,已知圓O:ρ=cosθ+sinθ和直線l:ρsin(θ﹣ ![]() )=
)= ![]() .
.
(1)求圓O和直線l的直角坐標方程;
(2)當θ∈(0,π)時,求直線l與圓O公共點的極坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學為調研學生在A,B兩家餐廳用餐的滿意度,從在A,B兩家餐廳都用過餐的學生中隨機抽取了100人,每人分別對這兩家餐廳進行評分,滿分均為60分.
整理評分數據,將分數以![]() 為組距分成
為組距分成![]() 組:
組: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到A餐廳分數的頻率分布直方圖,和B餐廳分數的頻數分布表:
,得到A餐廳分數的頻率分布直方圖,和B餐廳分數的頻數分布表:
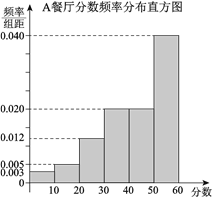
B餐廳分數頻數分布表 | |
分數區間 | 頻數 |
|
|
|
|
|
|
|
|
|
|
|
|
定義學生對餐廳評價的“滿意度指數”如下:
分數 |
|
|
|
滿意度指數 |
|
|
|
(Ⅰ)在抽樣的100人中,求對A餐廳評價“滿意度指數”為![]() 的人數;
的人數;
(Ⅱ)從該校在A,B兩家餐廳都用過餐的學生中隨機抽取1人進行調查,試估計其對A餐廳評價的“滿意度指數”比對B餐廳評價的“滿意度指數”高的概率;
(Ⅲ)如果從A,B兩家餐廳中選擇一家用餐,你會選擇哪一家?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com