
【題目】設向量 ![]() ,
, ![]() ,x∈R,記函數
,x∈R,記函數 ![]() .
.
(1)求函數f(x)的單調遞增區間;
(2)在銳角△ABC中,角A,B,C的對邊分別為a,b,c.若 ![]() ,
, ![]() ,求△ABC面積的最大值.
,求△ABC面積的最大值.
【答案】
(1)解:∵ ![]() =sinxcosx+
=sinxcosx+ ![]() (sinx﹣cosx)(sinx+cosx)=
(sinx﹣cosx)(sinx+cosx)= ![]() sin2x﹣
sin2x﹣ ![]() cos2x=sin(2x﹣
cos2x=sin(2x﹣ ![]() ),
),
∴令2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,解得:kπ﹣
,k∈Z,解得:kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
∴函數f(x)的單調遞增區間為:[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
(2)解:∵ ![]() ,
,
∴sin(2A﹣ ![]() )=
)= ![]() ,結合△ABC為銳角三角形,可得:2A﹣
,結合△ABC為銳角三角形,可得:2A﹣ ![]() =
= ![]() ,
,
∴A= ![]() ,
,
∵在△ABC中,由余弦定理a2=b2+c2﹣2bccosA,可得:2=b2+c2﹣ ![]() bc≥(2﹣
bc≥(2﹣ ![]() )bc,(當且僅當b=c時等號成立)
)bc,(當且僅當b=c時等號成立)
∴bc≤ ![]() =2+
=2+ ![]() ,
,
又∵sinA=sin ![]() =
= ![]() ,
,
∴S△ABC= ![]() bcsinA=
bcsinA= ![]() bc≤
bc≤ ![]() (2+
(2+ ![]() )=
)= ![]() ,(當且僅當b=c時等號成立)
,(當且僅當b=c時等號成立)
∴△ABC面積的最大值為 ![]()
【解析】(1)利用平面向量數量積的運算,三角函數恒等變換的應用化簡可求f(x)=sin(2x﹣ ![]() ),令2kπ﹣
),令2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,即可解得f(x)的單調遞增區間.(2)由已知可求sin(2A﹣
,k∈Z,即可解得f(x)的單調遞增區間.(2)由已知可求sin(2A﹣ ![]() )=
)= ![]() ,結合△ABC為銳角三角形,可得A,利用余弦定理,基本不等式可求bc≤2+
,結合△ABC為銳角三角形,可得A,利用余弦定理,基本不等式可求bc≤2+ ![]() ,進而利用三角形面積公式即可計算得解.
,進而利用三角形面積公式即可計算得解.
【考點精析】認真審題,首先需要了解余弦定理的定義(余弦定理:![]() ;
;![]() ;
;![]() ).
).


科目:高中數學 來源: 題型:
【題目】PM2.5是指大氣中直徑小于或等于2.5微米的顆粒物,也稱為可入肺顆粒物.如圖是根據環保部門某日早6點至晚9點在惠農縣、平羅縣兩個地區附近的PM2.5監測點統計的數據(單位:毫克/立方米)列出的莖葉圖,惠農縣、平羅縣兩個地區濃度的方差較小的是( ) 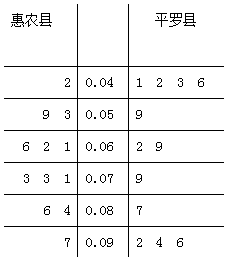
A.惠農縣
B.平羅縣
C.惠農縣、平羅縣兩個地區相等
D.無法確定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(x﹣2)lnx﹣ax+1.
(1)若f(x)在區間(1,+∞)上單調遞增,求實數a的取值范圍;
(2)若存在唯一整數x0 , 使得f(x0)<0成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知D,E是△ABC邊BC的三等分點,點P在線段DE上,若 ![]() =x
=x ![]() +y
+y ![]() ,則xy的取值范圍是( )
,則xy的取值范圍是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為 ![]() (t為參數),在以坐標原點為極點,x軸的正半軸為極軸的極坐標中,圓C的方程為ρ=4cosθ.
(t為參數),在以坐標原點為極點,x軸的正半軸為極軸的極坐標中,圓C的方程為ρ=4cosθ.
(Ⅰ)求l的普通方程和C的直角坐標方程;
(Ⅱ)當φ∈(0,π)時,l與C相交于P,Q兩點,求|PQ|的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC﹣A1B1C1中,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=2,P,Q分別為棱AA1 , AC的中點. 
(1)在平面ABC內過點A作AM∥平面PQB1交BC于點M,并寫出作圖步驟,但不要求證明;
(2)若側面ACC1A1⊥側面ABB1A1 , 求直線A1C1與平面PQB1所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數 ![]() ,記Ik=|fk(a2)﹣fk(a1)|+|fk(a3)﹣fk(a2)|++|fk(a2016)﹣fk(a2015)|,k=1,2,則( )
,記Ik=|fk(a2)﹣fk(a1)|+|fk(a3)﹣fk(a2)|++|fk(a2016)﹣fk(a2015)|,k=1,2,則( )
A.I1<I2
B.I1>I2
C.I1=I2
D.I1 , I2大小關系不確定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com