已知函數f（x）=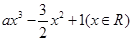
，其中a>0，
（Ⅰ）若a=1，求曲線y=f（x）在點（2，f（2））處的切線方程；
（Ⅱ）若在區間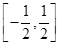
上，f（x）>0恒成立，求a的取值范圍。
（Ⅰ）y=6x-9；（Ⅱ）a的范圍為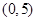
。
解析試題分析：（Ⅰ）解：當a=1時，f（x）=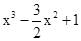
，f（2）=3；
=
, 
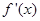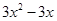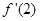=6.
所以曲線y=f（x）在點（2，f（2））處的切線方程為y-3=6（x-2），即y=6x-9
（Ⅱ）解：=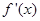
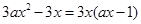.令f’(x)=0，解得x=0或x=
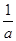. 5分
以下分兩種情況討論：
（1）若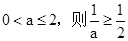
，當x變化時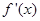，，f（x）的變化情況如表：
當x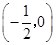 
0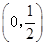 
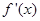
+ 0 - f（x） 
極大值 
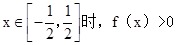等價于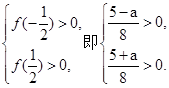
解不等式組得-5<a<5.因此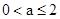
.
若a>2，則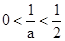
.當x變化時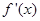，, f(x)的變化情況如下表：
，
，其中
是
的導函數．
的一切
的值，都有
，求實數
的取值范圍；
，當實數
在什么范圍內變化時，函數
的圖象與直線
只有一個公共點．
.
，求a的值；
時，求函數
的單調區間；
，
恒成立，求實數
的取值范圍.
.
處的切線方程；
，若在[1,e]上至少存在一點
，使得
成立，求實
.
在
和
處取得極值，試求
的值；
時，
恒成立，求c的取值范圍.
為
的極值點，求實數
的值；
在
上為增函數，求實數
時，方程
有實根，求實數
的最大值。
(x∈R)在區間[－1，1]上是增函數.
的兩個非零實根為x1、x2.試問：是否存在實數m，使得不等式m2+tm+1≥|x1－x2|對任意a∈A及t∈[－1，1]恒成立？若存在，求m的取值范圍；若不存在，請說明理由.
，
在
上的最小值；
與
的圖像恰有一個公共點，求實數a的值；
有兩個不同的極值點
，且
，求實數a的取值范圍。