
【題目】某生活超市有一專柜預代理銷售甲乙兩家公司的一種可相互替代的日常生活用品.經過一段時間分別單獨試銷甲乙兩家公司的商品,從銷售數據中隨機各抽取50天,統計每日的銷售數量,得到如下的頻數分布條形圖.甲乙兩家公司給該超市的日利潤方案為:甲公司給超市每天基本費用為90元,另外每銷售一件提成1元;乙公司給超市每天的基本費用為130元,每日銷售數量不超過83件沒有提成,超過83件的部分每件提成10元.
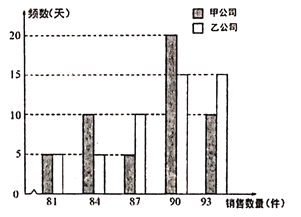
(Ⅰ)求乙公司給超市的日利潤![]() (單位:元)與日銷售數量
(單位:元)與日銷售數量![]() 的函數關系;
的函數關系;
(Ⅱ)若將頻率視為概率,回答下列問題:
(1)求甲公司產品銷售數量不超過87件的概率;
(2)如果僅從日均利潤的角度考慮,請你利用所學過的統計學知識為超市作出抉擇,選擇哪家公司的產品進行銷售?并說明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)(1)
;(Ⅱ)(1)![]() ;(2)超市應代理銷售乙公司的產品較為合適.
;(2)超市應代理銷售乙公司的產品較為合適.
【解析】
(Ⅰ)分別在![]() 和
和![]() 兩種情況下得到關系式,進而得到結果;
兩種情況下得到關系式,進而得到結果;
(Ⅱ)(1)利用頻率的計算方式可求得對應的概率;
(2)分別計算甲、乙兩公司給到超市的日利潤的平均數,選擇平均數較大的產品進行銷售.
(Ⅰ)當![]() 時,
時,![]() 元;
元;
當![]() 時,
時,![]() ;
;
![]() 乙公司給超市的日利潤
乙公司給超市的日利潤![]() (單位:元)與銷售數量
(單位:元)與銷售數量![]() 的函數關系為:
的函數關系為:![]() .
.
(Ⅱ)(1)記事件![]() :“甲公司產品的銷售數量不超過87件”,
:“甲公司產品的銷售數量不超過87件”,
則![]() ;
;
(2)甲公司給超市的日利潤為![]() 元,
元,
則![]() 的所有可能取值為
的所有可能取值為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() (元);
(元);
設乙公司給超市的日利潤為![]() 元,
元,
則![]() 的所有可能取值為
的所有可能取值為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
則![]() (元);
(元);
![]() ,所以超市應代理銷售乙公司的產品較為合適.
,所以超市應代理銷售乙公司的產品較為合適.


 精英口算卡系列答案
精英口算卡系列答案科目:高中數學 來源: 題型:
【題目】在某地區某高傳染性病毒流行期間,為了建立指標顯示校情已受控制,以便向該地區居眾顯示可以過正常生活,有公共衛生專家建議的指標是“連續![]() 天每天新增感染人數不超過
天每天新增感染人數不超過![]() 人”,根據連續
人”,根據連續![]() 天的新增病例數計算,下列各項選項中,一定符合上述指標的是( )
天的新增病例數計算,下列各項選項中,一定符合上述指標的是( )
①平均數![]() ;
;
②標準差![]() ;
;
③平均數![]() ;且標準差
;且標準差![]() ;
;
④平均數![]() ;且極差小于或等于
;且極差小于或等于![]() ;
;
⑤眾數等于![]() 且極差小于或等于
且極差小于或等于![]() .
.
A.①②B.③④C.③④⑤D.④⑤
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市9年前分別同時開始建設物流城和濕地公園,物流城3年建設完成,建成后若年投入x億元,該年產生的經濟凈效益為![]() 億元;濕地公園4年建設完成,建成后的5年每年投入見散點圖.公園建成后若年投入x億元,該年產生的經濟凈效益為
億元;濕地公園4年建設完成,建成后的5年每年投入見散點圖.公園建成后若年投入x億元,該年產生的經濟凈效益為![]() 億元.
億元.

(1)對濕地公園,請在![]() 中選擇一個合適模型,求投入額x與投入年份n的回歸方程;
中選擇一個合適模型,求投入額x與投入年份n的回歸方程;
(2)從建設開始的第10年,若對物流城投入0.25億元,預測這一年物流城和濕地公園哪個產生的年經濟凈效益高?請說明理由.
參考數據及公式:![]() ,
,![]() ;當
;當![]() 時,
時,![]() ,
,![]() ,回歸方程中的
,回歸方程中的![]() ;回歸方程
;回歸方程![]() 斜率與截距
斜率與截距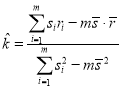 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在長方體![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一條線段,且
上的一條線段,且![]() ,
,![]() 是
是![]() 的中點,
的中點,![]() 是棱
是棱![]() 上的動點,則
上的動點,則
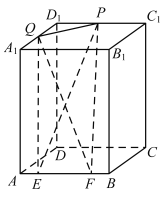
①四面體![]() 的體積為定值
的體積為定值
②直線![]() 到平面
到平面![]() 的距離為定值
的距離為定值
③點![]() 到直線
到直線![]() 的距離為定值
的距離為定值
④直線![]() 與平面
與平面![]() 所成的角為定值
所成的角為定值
其中正確結論的編號是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在長方體![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一條線段,且
上的一條線段,且![]() ,
,![]() 是
是![]() 的中點,
的中點,![]() 是棱
是棱![]() 上的動點,則
上的動點,則
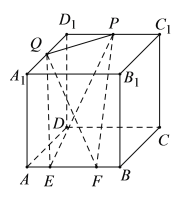
①四面體![]() 的體積為定值
的體積為定值
②直線![]() 到平面
到平面![]() 的距離為定值
的距離為定值
③點![]() 到直線
到直線![]() 的距離為定值
的距離為定值
④直線![]() 與平面
與平面![]() 所成的角為定值
所成的角為定值
其中正確結論的編號是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產了一批零件,從中隨機抽取100個作為樣本,測出它們的長度(單位:厘米),按數據分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 5組,得到如圖所示的頻率分布直方圖.以這100個零件的長度在各組的頻率代替整批零件長度在該組的概率.
5組,得到如圖所示的頻率分布直方圖.以這100個零件的長度在各組的頻率代替整批零件長度在該組的概率.
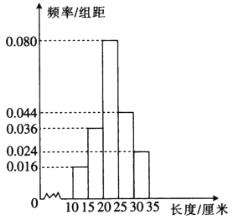
(1)估計該工廠生產的這批零件長度的平均值(同一組中的每個數據用該組區間的中點值代替);
(2)規定零件長度在區間![]() 內的零件為優等品,從這批零件中隨機抽取3個,記抽到優等品的個數為X,求X的分布列和數學期望.
內的零件為優等品,從這批零件中隨機抽取3個,記抽到優等品的個數為X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,已知曲線![]() (
(![]() 為參數),直線
為參數),直線![]() (
(![]() 為參數,
為參數, ![]() ),直線
),直線![]() 與曲線
與曲線![]() 相切于點
相切于點![]() ,以坐標原點
,以坐標原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系.
軸的非負半軸為極軸建立極坐標系.
(1)求曲線![]() 的極坐標方程及點
的極坐標方程及點![]() 的極坐標;
的極坐標;
(2)曲線![]() 的直角坐標方程為
的直角坐標方程為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于在
交于在![]() ,
,![]() 兩點,記
兩點,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某運動制衣品牌為了成衣尺寸更精準,現選擇15名志愿者,對其身高和臂展進行測量(單位:厘米),左圖為選取的15名志愿者身高與臂展的折線圖,右圖為身高與臂展所對應的散點圖,并求得其回歸方程為![]() ,以下結論中不正確的為
,以下結論中不正確的為


A. 15名志愿者身高的極差小于臂展的極差
B. 15名志愿者身高和臂展成正相關關系,
C. 可估計身高為190厘米的人臂展大約為189.65厘米,
D. 身高相差10厘米的兩人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在等比數列![]() 中,已知
中,已知![]() 設數列
設數列![]() 的前n項和為
的前n項和為![]() ,且
,且![]()
(1)求數列![]() 通項公式;
通項公式;
(2)證明:數列![]() 是等差數列;
是等差數列;
(3)是否存在等差數列![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() ?若存在,求出所有符合題意的等差數列
?若存在,求出所有符合題意的等差數列![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com