Question

【題目】傳承傳統(tǒng)文化再掀熱潮，央視科教頻道以詩詞知識競賽為主的《中國詩詞大會》火爆熒屏。將中學組和大學組的參賽選手按成績分為優(yōu)秀、良好、一般三個等級，隨機從中抽取了100名選手進行調(diào)查，下面是根據(jù)調(diào)查結(jié)果繪制的選手等級人數(shù)的條形圖.

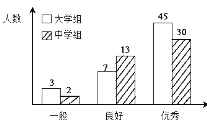
(Ⅰ)若將一般等級和良好等級合稱為合格等級，根據(jù)已知條件完成下面的2×2列聯(lián)表，并據(jù)此資料你是否有95﹪的把握認為選手成績“優(yōu)秀”與文化程度有關(guān)？

	優(yōu)秀	合格	合計
大學組
中學組
合計

注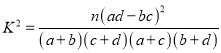： ，其中.

	0.10	0.05	0. 005
	2.706	3.841	7.879

(Ⅱ)若江西參賽選手共80人，用頻率估計概率，試估計其中優(yōu)秀等級的選手人數(shù)；

（Ⅲ）如果在優(yōu)秀等級的選手中取4名，在良好等級的選手中取2名，再從這6人中任選3人組成一個比賽團隊，求所選團隊中的有2名選手的等級為優(yōu)秀的概率.

Answer 1

【答案】（Ⅰ）見解析; （Ⅱ）60人；（Ⅲ） .

【解析】試題分析：（Ⅰ）由條形圖可知2×2列聯(lián)表，計算k2，與臨界值比較，即可得出結(jié)論；

（Ⅱ）由條形圖知，所抽取的100人中，優(yōu)秀等級有75人，故優(yōu)秀率為，可得優(yōu)秀等級的選手人數(shù)；

（Ⅲ）記優(yōu)秀等級中4人分別為A，B，C，D，良好等級中的兩人為E，F(xiàn)，利用古典概型求概率公式求解即可.

試題解析：

（Ⅰ）由條形圖可知2×2列聯(lián)表如下

	優(yōu)秀	合格	合計
大學組	45	10	55
中學組	30	15	45
合計	75	25	100

沒有95﹪的把握認為優(yōu)秀與文化程度有關(guān).

（Ⅱ）由條形圖知，所抽取的100人中，優(yōu)秀等級有75人，故優(yōu)秀率為.

所有參賽選手中優(yōu)秀等級人數(shù)約為人.

（Ⅲ）記優(yōu)秀等級中4人分別為A，B，C，D，良好等級中的兩人為E，F(xiàn)，則任取3人的取法有ABC，ABD，ABE，ABF，ACD，ACE，ACF，ADE，ADF，AEF，BCD，BCE，BCF，BDE，BDF，BEF，CDE，CDF，CEF，DEF共20種，其中有2名選手的等級為優(yōu)秀的有ABE，ABF，ACE，ACF，ADE，ADF，BCE，BCF，BDE，BDF，CDE，CDF共12種，所以所選團隊中的有2名選手的等級為優(yōu)秀的概率為.