
【題目】如圖,四棱錐P-ABCD中,PA⊥底面ABCD,底面ABCD為梯形,AD∥BC,CD⊥BC,AD=2,AB=BC=3,PA=4,M為AD的中點,N為PC上一點,且PC=3PN.
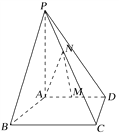
(1)求證:MN∥平面PAB;
(2)求點M到平面PAN的距離.
【答案】(1)證明見解析;(2) ![]() .
.
【解析】試題分析:(1)作NH∥BC交PB于點H,連接AH,得四邊形AMNH為平行四邊形,所以MN∥AH,所以MN∥平面PAB;(2)由等體積法得VM-PAC=VP-AMC,即4![]() h=
h=![]() ×4,所以h=
×4,所以h=![]() 。
。
試題解析:
(1)在平面PBC內作NH∥BC交PB于點H,連接AH,
在△PBC中,NH∥BC,且NH=![]() BC=1,AM=
BC=1,AM=![]() AD=1.
AD=1.
又AD∥BC,∴NH∥AM且NH=AM,
∴四邊形AMNH為平行四邊形,∴MN∥AH,
又AH平面PAB,MN平面PAB,
∴MN∥平面PAB.
(2)連接AC,MC,PM,平面PAN即為平面PAC,設點M到平面PAC的距離為h.
由題意可得CD=2![]() ,AC=2
,AC=2![]() ,
,
∴S△PAC=![]() PA·AC=4
PA·AC=4![]() ,
,
∴S△AMC=![]() AM·CD=
AM·CD=![]() ,
,
由VM-PAC=VP-AMC,得![]() S△PAC·h=
S△PAC·h=![]() S△AMC·PA,
S△AMC·PA,
即4![]() h=
h=![]() ×4,∴h=
×4,∴h=![]() ,
,
∴點M到平面PAN的距離為![]() .
.


 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案 初中暑期銜接系列答案
初中暑期銜接系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() sin 2x-
sin 2x-![]() cos2x.
cos2x.
(1)求f(x)的周期和最小值;
(2)將函數f(x)的圖像上每一點的橫坐標伸長到原來的兩倍(縱坐標不變),再把所得圖像上的所有點向上平移![]() 個單位,得到函數g(x)的圖像,當
個單位,得到函數g(x)的圖像,當![]() 時,求g(x)的值域.
時,求g(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知在極坐標系和直角坐標系中,極點與直角坐標系的原點重合,極軸與![]() 軸的非負半軸重合,曲線
軸的非負半軸重合,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)求曲線![]() 的直角坐標方程和曲線
的直角坐標方程和曲線![]() 的普通方程;
的普通方程;
(2)判斷曲線![]() 與曲線
與曲線![]() 的位置關系,若兩曲線相交,求出兩交點間的距離.
的位置關系,若兩曲線相交,求出兩交點間的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著醫院對看病掛號的改革,網上預約成為了當前最熱門的就診方式,這解決了看病期間病人插隊以及醫生先治療熟悉病人等諸多問題;某醫院研究人員對其所在地區年齡在10~60歲間的![]() 位市民對網上預約掛號的了解情況作出調查,并將被調查的人員的年齡情況繪制成頻率分布直方圖,如下圖所示.
位市民對網上預約掛號的了解情況作出調查,并將被調查的人員的年齡情況繪制成頻率分布直方圖,如下圖所示.

(Ⅰ)若被調查的人員年齡在20~30歲間的市民有300人,求被調查人員的年齡在40歲以上(含40歲)的市民人數;
(Ⅱ)若按分層抽樣的方法從年齡在![]() 以內及
以內及![]() 以內的市民中隨機抽取5人,再從這5人中隨機抽取2人進行調研,求抽取的2人中,至多1人年齡在
以內的市民中隨機抽取5人,再從這5人中隨機抽取2人進行調研,求抽取的2人中,至多1人年齡在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據國家環保部新修訂的《環境空氣質量標準》規定:居民區![]() 的年平均濃度不得超過3S微克/立方米,
的年平均濃度不得超過3S微克/立方米, ![]() 的24小時平均濃度不得超過75微克/立方米.某市環保局隨機抽取了一居民區2016年20天
的24小時平均濃度不得超過75微克/立方米.某市環保局隨機抽取了一居民區2016年20天![]() 的24小時平均濃度(單位:微克/立方米)的監測數據,數據統計如圖表:
的24小時平均濃度(單位:微克/立方米)的監測數據,數據統計如圖表:
組別 |
| 頻數(天) | 頻率 |
第一組 |
| 3 | 0.15 |
第二組 |
| 12 | 0.6 |
第三組 |
| 3 | 0.15 |
第四組 |
| 2 | 0.1 |
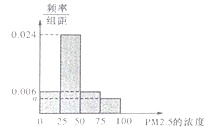
(Ⅰ)將這20天的測量結果按表中分組方法繪制成的樣本頻率分布直方圖如圖.
(ⅰ)求圖中![]() 的值;
的值;
(ⅱ)在頻率分布直方圖中估算樣本平均數,并根據樣本估計總體的思想,從![]() 的年平均度考慮,判斷該居民區的環境質量是否需要改善?并說明理由.
的年平均度考慮,判斷該居民區的環境質量是否需要改善?并說明理由.
(Ⅱ)將頻率視為概率,對于2016年的某3天,記這3天中該居民區![]() 的24小時平均濃度符合環境空氣質量標準的天數為
的24小時平均濃度符合環境空氣質量標準的天數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() sinωxcosωx-cos2ωx+
sinωxcosωx-cos2ωx+![]() (ω>0),經化簡后利用“五點法”畫其在某一周期內的圖象時,列表并填入的部分數據如下表:
(ω>0),經化簡后利用“五點法”畫其在某一周期內的圖象時,列表并填入的部分數據如下表:
x | ① |
|
| ||
f(x) | 0 | 1 | 0 | -1 | 0 |
(1)請直接寫出①處應填的值,并求函數f(x)在區間![]() 上的值域;
上的值域;
(2)△ABC的內角A,B,C所對的邊分別為a,b,c,已知f(A+![]() )=1,b+c=4,a=
)=1,b+c=4,a=![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com