
【題目】定義在R上的增函數y=f(x)對任意x,y∈R都有f(x+y)=f(x)+f(y).
(1)求f(0);
(2)求證:f(x)為奇函數;
(3)若f(k3x)+f(3x﹣9x﹣4)<0對任意x∈R恒成立,求實數k的取值范圍.
【答案】
(1)解:令x=y=0,得f(0+0)=f(0)+f(0),即f(0)=0
(2)解:證明:令y=﹣x,則f(x﹣x)=f(x)+f(﹣x)=0,
即f(﹣x)=﹣f(x),∴函數f(x)是奇函數
(3)解:又函數f(x)在R上的是單調遞增函數,
由f(k3x)+f(3x﹣9x﹣4)<0,
得f(k3x)<﹣f(3x﹣9x﹣4)=f(﹣3x+9x+4),
即k3x<﹣3x+9x+4恒成立,
∴k< ![]() =3x+
=3x+ ![]() ﹣1,
﹣1,
∵3x+ ![]() ﹣1≥2
﹣1≥2 ![]() ﹣1=4﹣1=3,
﹣1=4﹣1=3,
當且僅當3x= ![]() ,即x=log32時取等號,
,即x=log32時取等號,
∴k<3,
即實數k的取值范圍是(﹣∞,3)
【解析】(1)令x=y=0,進行求解,(2)利用函數奇偶性的定義,結合抽象函數,證明f(x)為奇函數;(3)利用函數的單調性和奇偶性解不等式即可.


科目:高中數學 來源: 題型:
【題目】甲廠根據以往的生產銷售經驗得到下面有關生產銷售的統計規律:每生產產品x(百臺),其總成本為G(x)(萬元),其中固定成本為3萬元,并且每生產1百臺的生產成本為1萬元(總成本=固定成本+生產成本),銷售收入R(x)= ![]() ,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,請完成下列問題:
,假定該產品產銷平衡(即生產的產品都能賣掉),根據上述統計規律,請完成下列問題:
(1)寫出利潤函數y=f(x)的解析式(利潤=銷售收入﹣總成本);
(2)甲廠生產多少臺新產品時,可使盈利最多?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題錯誤的是( )
A.命題“若x2﹣3x+2=0,則x=1”的逆否命題為“若x≠1,則x2﹣3x+2≠0”
B.若p∧q為假命題,則p,q均為假命題
C.對命題P:存在x∈R,使得x2+x+1<0,則¬p為:任意x∈R,均有x2+x+1≥0
D.“x>2”是“x2﹣3x+2>0”的充分不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本題滿分12分) 已知集合![]() 在平面直角坐標系中,點M的坐標為(x,y) ,其中
在平面直角坐標系中,點M的坐標為(x,y) ,其中![]() 。
。
(1)求點M不在x軸上的概率;
(2)求點M正好落在區域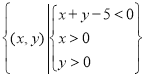 上的概率。
上的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sin(ωx+ ![]() )(ω>0)的圖象與y=2的圖象的兩相鄰交點的距離為π,要得到y=2sinωx的圖象,只需把y=f(x)的圖象( )
)(ω>0)的圖象與y=2的圖象的兩相鄰交點的距離為π,要得到y=2sinωx的圖象,只需把y=f(x)的圖象( )
A.向右平移 ![]()
B.向左平移 ![]()
C.向左平移 ![]()
D.向右平移 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業有兩個分廠生產某種零件,按規定內徑尺寸(單位:mm)的值落在[29.94,30.06)的零件為優質品.從兩個分廠生產的零件中各抽出了500件,量其內徑尺寸,得結果如下表:
甲廠:
分組 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
頻數 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
乙廠:
分組 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
頻數 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
(1)試分別估計兩個分廠生產的零件的優質品率;
(2)由以上統計數據填下面![]() 列聯表,并問是否有
列聯表,并問是否有![]() 的把握認為“兩個分廠生產的零件的質量有差異”.
的把握認為“兩個分廠生產的零件的質量有差異”.
甲 廠 | 乙 廠 | 合計 | |
優質品 | |||
非優質品 | |||
合計 |
附: 
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:如果函數f(x)在[a,b]上存在x1 , x2(a<x1<x2<b)滿足f′(x1)= ![]() ,f′(x2)
,f′(x2) ![]() ,則稱函數f(x)是[a,b]上的“雙中值函數”.已知函數f(x)=x3﹣x2+a是[0,a]上“雙中值函數”,則實數a的取值范圍是( )
,則稱函數f(x)是[a,b]上的“雙中值函數”.已知函數f(x)=x3﹣x2+a是[0,a]上“雙中值函數”,則實數a的取值范圍是( )
A.( ![]() ,
, ![]() )
)
B.(0,1)
C.( ![]() ,1)
,1)
D.( ![]() ,1)
,1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>b>0)過點A(﹣
=1(a>b>0)過點A(﹣ ![]() ,
, ![]() ),離心率為
),離心率為 ![]() ,點F1 , F2分別為其左右焦點.
,點F1 , F2分別為其左右焦點.
(1)求橢圓C的標準方程;
(2)若y2=4x上存在兩個點M,N,橢圓上有兩個點P,Q滿足,M,N,F2三點共線,P,Q,F2三點共線,且PQ⊥MN.求四邊形PMQN面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
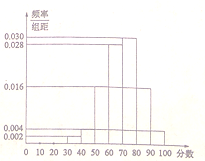
【題目】2016年某市政府出臺了“2020年創建全國文明城市(簡稱創文)”的具體規劃,今日,作為“創文”項目之一的“市區公交站點的重新布局及建設”基本完成,市有關部門準備對項目進行調查,并根據調查結果決定是否驗收,調查人員分別在市區的各公交站點隨機抽取若干市民對該項目進行評分,并將結果繪制成如圖所示的頻率分布直方圖,相關規則為:①調查對象為本市市民,被調查者各自獨立評分;②采用百分制評分, ![]() 內認定為滿意,80分及以上認定為非常滿意;③市民對公交站點布局的滿意率不低于60%即可進行驗收;④用樣本的頻率代替概率.
內認定為滿意,80分及以上認定為非常滿意;③市民對公交站點布局的滿意率不低于60%即可進行驗收;④用樣本的頻率代替概率.
(1)求被調查者滿意或非常滿意該項目的頻率;
(2)若從該市的全體市民中隨機抽取3人,試估計恰有2人非常滿意該項目的概率;
(3)已知在評分低于60分的被調查者中,老年人占![]() ,現從評分低于60分的被調查者中按年齡分層抽取9人以便了解不滿意的原因,并從中選取2人擔任群眾督察員,記
,現從評分低于60分的被調查者中按年齡分層抽取9人以便了解不滿意的原因,并從中選取2人擔任群眾督察員,記![]() 為群眾督查員中老年人的人數,求隨機變量
為群眾督查員中老年人的人數,求隨機變量![]() 的分布列及其數學期望
的分布列及其數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com