
【題目】如圖,已知圓N:x2+(y+ ![]() )2=36,P是圓N上的點,點Q在線段NP上,且有點D(0,
)2=36,P是圓N上的點,點Q在線段NP上,且有點D(0, ![]() )和DP上的點M,滿足
)和DP上的點M,滿足 ![]() =2
=2 ![]() ,
, ![]()
![]() =0.
=0. 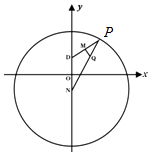
(1)當P在圓上運動時,求點Q的軌跡方程;
(2)若斜率為 ![]() 的直線l與(1)中所求Q的軌跡交于不同兩點A、B,又點C(
的直線l與(1)中所求Q的軌跡交于不同兩點A、B,又點C( ![]() ,2),求△ABC面積最大值時對應的直線l的方程.
,2),求△ABC面積最大值時對應的直線l的方程.
【答案】
(1)解:由題意,MQ是線段DP的中垂線,∴|NP|=|NQ|+|QP|=|QN|+|QD|=6>|DN|=2 ![]() ,
,
∴Q的軌跡是以D,N為焦點的橢圓,且c= ![]() ,a=3,b=2,
,a=3,b=2,
∴求點Q的軌跡方程是 ![]() =1
=1
(2)解:設l:y= ![]() x+m,A(x1,y1),B(x2,y2),
x+m,A(x1,y1),B(x2,y2),
與橢圓聯立,可得9x2+6mx+2m2﹣18=0,
x1+x2=﹣ ![]() m,x1x2=
m,x1x2= ![]() (2m2﹣18),
(2m2﹣18),
|AB|= ![]()
![]() =
= ![]() ,
,
C( ![]() ,2)到直線l的距離d=
,2)到直線l的距離d= ![]() ,
,
S= ![]() =
= ![]() ,
,
∴m=±3時,S最大,此時直線l的方程為y= ![]() x±3
x±3
【解析】(1)當P在圓上運動時,利用橢圓的定義,求點Q的軌跡方程;(2)△ABC的面積取到最大值問題,要先建立關于某個自變量的函數,后再求此函數的最大值即可.


 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:高中數學 來源: 題型:
【題目】[選修4-5:不等式選講]
已知函數f(x)=﹣x2+ax+4,g(x)=|x+1|+|x﹣1|.(10分)
(1)當a=1時,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[﹣1,1],求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),且直線
為參數),且直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,以直角坐標系的原點為極點,以
兩點,以直角坐標系的原點為極點,以![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2) 已知點![]() 的極坐標為
的極坐標為![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)g(x)分別是定義在R上的偶函數和奇函數,且f(x)+g(x)=23x.
(1)證明:f(x)-g(x)=23-x,并求函數f(x),g(x)的解析式;
(2)解關于x不等式:g(x2+2x)+g(x-4)>0;
(3)若對任意x∈R,不等式f(2x)≥mf(x)-4恒成立,求實數m的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學開設甲、乙、丙三門選修課,學生是否選修哪門課互不影響,已知某學生只選修甲的概率為0.08,只選修甲和乙的概率是0.12,至少選修一門的概率是0.88,用![]() 表示該學生選修的課程門數和沒有選修的課程門數的乘積.
表示該學生選修的課程門數和沒有選修的課程門數的乘積.
(1)記“函數![]() 為
為![]() 上的偶函數”為事件
上的偶函數”為事件![]() ,求事件
,求事件![]() 的概率;
的概率;
(2)求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解學生喜歡校內、校外開展活動的情況,某中學一課外活動小組在學校高一年級進行了問卷調查,問卷共100道題,每題1分,總分100分,該課外活動小組隨機抽取了200名學生的問卷成績(單位:分)進行統計,將數據按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成五組,繪制的頻率分布直方圖如圖所示,若將不低于60分的稱為
分成五組,繪制的頻率分布直方圖如圖所示,若將不低于60分的稱為![]() 類學生,低于60分的稱為
類學生,低于60分的稱為![]() 類學生.
類學生.

(1)根據已知條件完成下面![]() 列聯表,能否在犯錯誤的概率不超過
列聯表,能否在犯錯誤的概率不超過![]() 的前提下認為性別與是否為
的前提下認為性別與是否為![]() 類學生有關系?
類學生有關系?
|
| 合計 | |
男 | 110 | ||
女 | 50 | ||
合計 |
(2)將頻率視為概率,現在從該校高一學生中用隨機抽樣的方法每次抽取1人,共抽取3次,記被抽取的3人中![]() 類學生的人數為
類學生的人數為![]() ,若每次抽取的結果是相互獨立的,求
,若每次抽取的結果是相互獨立的,求![]() 的分布列、期望
的分布列、期望![]() 和方差
和方差![]() .
.
參考公式:![]() ,其中
,其中![]() .
.
參考臨界值:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(1-2x)(x2-2).
(1)求f(x)的單調區間和極值;
(2)若直線y=4x+b是函數y=f(x)圖象的一條切線,求b的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com