
【題目】隨著網(wǎng)絡(luò)營(yíng)銷(xiāo)和電子商務(wù)的興起,人們的購(gòu)物方式更具多樣化.某調(diào)查機(jī)構(gòu)隨機(jī)抽取8名購(gòu)物者進(jìn)行采訪(fǎng),4名男性購(gòu)物者中有3名傾向于網(wǎng)購(gòu),1名傾向于選擇實(shí)體店,4名女性購(gòu)物者中有2名傾向于選擇網(wǎng)購(gòu),2名傾向于選擇實(shí)體店.
(1)若從8名購(gòu)物者中隨機(jī)抽取2名,其中男女各一名,求至少1名傾向于選擇實(shí)體店的概率:
(2)若從這8名購(gòu)物者中隨機(jī)抽取3名,設(shè)X表示抽到傾向于選擇網(wǎng)購(gòu)的男性購(gòu)物者的人數(shù),求X的分布列和數(shù)學(xué)期望.
【答案】(1)![]() (2)見(jiàn)解析
(2)見(jiàn)解析
【解析】分析:(1)根據(jù)獨(dú)立事件,可以求出沒(méi)有人傾向于選擇實(shí)體店的概率;利用對(duì)立事件的概率,可以求出解。
(2)根據(jù)離散型隨機(jī)變量的概率分布,列出分布列,即可求出數(shù)學(xué)期望。
詳解:(1)設(shè)“隨機(jī)抽取2名,其中男、女各一名,至少1名傾向于選擇實(shí)體店”為事件A,則![]() 表示“隨機(jī)抽取2名,其中男、女各一名,都傾向于選擇網(wǎng)購(gòu)”,
表示“隨機(jī)抽取2名,其中男、女各一名,都傾向于選擇網(wǎng)購(gòu)”,
則P(A)=1-P(![]() )=1-
)=1-![]() =
=![]() .
.
(2)X的所有可能取值為0,1,2,3,且P(X=k)=![]() ,
,
則P(X=0)=![]() ,P(X=1)=
,P(X=1)= ![]() ,
,
P(X=2)=![]() ,P(X=3)=
,P(X=3)=![]() .
.
所以X的分布列為
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以E(X)=0×![]() +l×
+l×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]()
(1)當(dāng)![]() 時(shí),討論函數(shù)
時(shí),討論函數(shù)![]() 零點(diǎn)的個(gè)數(shù);
零點(diǎn)的個(gè)數(shù);
(2)若![]() ,當(dāng)
,當(dāng)![]() =1時(shí),求證:
=1時(shí),求證:![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某工廠(chǎng)生產(chǎn)甲、乙兩種產(chǎn)品所得利潤(rùn)分別為![]() 和
和![]() (萬(wàn)元),它們與投入資金
(萬(wàn)元),它們與投入資金![]() (萬(wàn)元)的關(guān)系有如下公式:
(萬(wàn)元)的關(guān)系有如下公式:![]() ,
,![]() ,今將200萬(wàn)元資金投入生產(chǎn)甲、乙兩種產(chǎn)品,并要求對(duì)甲、乙兩種產(chǎn)品的投入資金都不低于25萬(wàn)元.
,今將200萬(wàn)元資金投入生產(chǎn)甲、乙兩種產(chǎn)品,并要求對(duì)甲、乙兩種產(chǎn)品的投入資金都不低于25萬(wàn)元.
(Ⅰ)設(shè)對(duì)乙種產(chǎn)品投入資金![]() (萬(wàn)元),求總利潤(rùn)
(萬(wàn)元),求總利潤(rùn)![]() (萬(wàn)元)關(guān)于
(萬(wàn)元)關(guān)于![]() 的函數(shù)關(guān)系式及其定義域;
的函數(shù)關(guān)系式及其定義域;
(Ⅱ)如何分配投入資金,才能使總利潤(rùn)最大,并求出最大總利潤(rùn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】數(shù)列![]()
滿(mǎn)足:![]() 或1(k=1,2,…,n-1).
或1(k=1,2,…,n-1).
對(duì)任意i,j,都存在s,t,使得![]() ,其中i,j,s,t∈{1,2,…,n}且兩兩不相等.
,其中i,j,s,t∈{1,2,…,n}且兩兩不相等.
(I)若m=2,寫(xiě)出下列三個(gè)數(shù)列中所有符合題目條件的數(shù)列的序號(hào);
①1,1,1,2,2,2; ②1,1,1,1,2,2,2,2; ③1,1,1,1,1,2,2,2,2
(II)記![]() .若m=3,求S的最小值;
.若m=3,求S的最小值;
(III)若m=2018,求n的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=(1-2x)(x2-2).
(1)求f(x)的單調(diào)區(qū)間和極值;
(2)若直線(xiàn)y=4x+b是函數(shù)y=f(x)圖象的一條切線(xiàn),求b的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=![]() (a、b∈R,a、b為常數(shù)),且y=f(x)在x=1處切線(xiàn)方程為y=x﹣1.
(a、b∈R,a、b為常數(shù)),且y=f(x)在x=1處切線(xiàn)方程為y=x﹣1.
(1)求a,b的值;
(2)設(shè)h(x)=![]() , k(x)=2h′(x)x2 , 求證:當(dāng)x>0時(shí),k(x)<
, k(x)=2h′(x)x2 , 求證:當(dāng)x>0時(shí),k(x)<![]() +
+![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列說(shuō)法中:
①若![]() ,滿(mǎn)足
,滿(mǎn)足![]() ,則
,則![]() 的最大值為4;
的最大值為4;
②若![]() ,則函數(shù)
,則函數(shù)![]() 的最小值為3;
的最小值為3;
③若![]() ,滿(mǎn)足
,滿(mǎn)足![]() ,則
,則![]() 的最大值為
的最大值為![]() ;
;
④若![]() ,滿(mǎn)足
,滿(mǎn)足![]() ,則
,則![]() 的最小值為2;
的最小值為2;
⑤函數(shù)![]() 的最小值為9.
的最小值為9.
正確的有________.(把你認(rèn)為正確的序號(hào)全部寫(xiě)上)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知變量![]() 之間的線(xiàn)性回歸方程為
之間的線(xiàn)性回歸方程為![]() ,且變量
,且變量![]() 之間的一組相關(guān)數(shù)據(jù)如表所示,則下列說(shuō)法錯(cuò)誤的是( )
之間的一組相關(guān)數(shù)據(jù)如表所示,則下列說(shuō)法錯(cuò)誤的是( )
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 變量![]() 之間呈現(xiàn)負(fù)相關(guān)關(guān)系
之間呈現(xiàn)負(fù)相關(guān)關(guān)系
B. ![]() 的值等于5
的值等于5
C. 變量![]() 之間的相關(guān)系數(shù)
之間的相關(guān)系數(shù)![]()
D. 由表格數(shù)據(jù)知,該回歸直線(xiàn)必過(guò)點(diǎn)(9,4)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,在平面直角坐標(biāo)系![]() 中,第一象限內(nèi)有定點(diǎn)
中,第一象限內(nèi)有定點(diǎn)![]() 和射線(xiàn)
和射線(xiàn)![]() ,已知
,已知![]() ,
,![]() 的傾斜角分別為
的傾斜角分別為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 軸上的動(dòng)點(diǎn)
軸上的動(dòng)點(diǎn)![]() 與
與![]() ,
,![]() 共線(xiàn).
共線(xiàn).
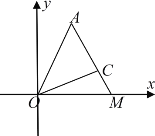
(1)求![]() 點(diǎn)坐標(biāo)(用
點(diǎn)坐標(biāo)(用![]() 表示);
表示);
(2)求![]() 面積
面積![]() 關(guān)于
關(guān)于![]() 的表達(dá)式
的表達(dá)式![]() ;
;
(3)求![]() 面積的最小時(shí)直線(xiàn)
面積的最小時(shí)直線(xiàn)![]() 的方程.
的方程.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com