Question

【題目】設直線與直線分別與橢圓交于點，且四邊形的面積為.

（1）求橢圓的方程；

（2）過橢圓上一點作橢圓的切線，設直線與橢圓相較于，兩點，為坐標原點，求的取值范圍.

Answer 1

【答案】（1）（2）

【解析】

聯立直線AB與橢圓的方程，解出x與y，由橢圓的對稱性可知四邊形ACBD為矩形，進而表示出矩形ACBD的面積為，從而得解；

分類討論，當直線l的斜率不存在，此時點P為橢圓的左或右頂點，易求得和，所以；

當直線l的斜率存在，設其方程為，點P的坐標為，M、N的坐標分別為，，兩次聯立直線與橢圓，分別可得到關于x的一元二次方程，結合直線l與橢圓相切，可得及，結合弦長公式，可得，然后作比，即可求得取值范圍．

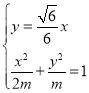由，解得，，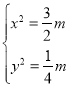

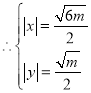由橢圓的對稱性可知，四邊形ACBD為矩形，且其面積，，

故橢圓的方程為．

當直線l的斜率不存在時，點P為橢圓的左或右頂點，其坐標為，

不妨取左頂點，即，此時，且直線l與x軸垂直，將代入得，，，

所以；

當直線l的斜率存在時，設其方程為，點P的坐標為，M、N的坐標分別為，，

聯立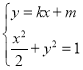，得，

直線l與橢圓相切，，

化簡整理得，，

由韋達定理知，，

，

聯立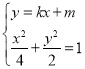，得，

由韋達定理知，，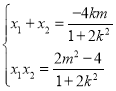

，

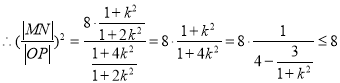，當且僅當時，等號成立，

綜上所述，的取值范圍為．