
【題目】如圖,在同一平面內,點P位于兩平行直線l1、l2兩側,且P到l1 , l2的距離分別為1,3,點M,N分別在l1 , l2上,| ![]() +
+ ![]() |=8,則
|=8,則 ![]()
![]() 的最大值為( )
的最大值為( ) 
A.15
B.12
C.10
D.9
【答案】A
【解析】解:由點P位于兩平行直線l1 , l2的同側,且A到l1 , l2的距離分別為1,3, 可得平行線l1、l2間的距離為2;
以直線l2為x軸,以過點P且與直線l2垂直的直線為y軸,
建立坐標系,如圖所示:
由題意可得點P(0,﹣1),直線l1的方程為y=2,
設點M(a,0)、點N(b,2),
∴ ![]() =(a,1)、
=(a,1)、 ![]() =(b,3),
=(b,3),
∴ ![]() +
+ ![]() =(a+b,4);
=(a+b,4);
∵| ![]() +
+ ![]() |=8,
|=8,
∴(a+b)2+16=64,
∴a+b=4 ![]() ,或a+b=﹣4
,或a+b=﹣4 ![]() ;
;
當a+b=4 ![]() 時,
時, ![]()
![]() =ab+3=a(4
=ab+3=a(4 ![]() ﹣a)+3=﹣a2+4
﹣a)+3=﹣a2+4 ![]() a+3,
a+3,
它的最大值為﹣ ![]() +4
+4 ![]() ×2
×2 ![]() +3=15;
+3=15;
當a+b=﹣3時, ![]() =ab+3=a(﹣4
=ab+3=a(﹣4 ![]() ﹣a)+3=﹣a2﹣4
﹣a)+3=﹣a2﹣4 ![]() a+3,
a+3,
它的最大值為﹣ ![]() ﹣4
﹣4 ![]() ×(﹣2
×(﹣2 ![]() )+3=15;
)+3=15;
綜上可得, ![]() 的最大值為15.
的最大值為15.
故選:A.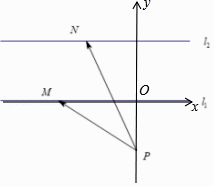


 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案 小天才課時作業系列答案
小天才課時作業系列答案科目:高中數學 來源: 題型:
【題目】為了解春季晝夜溫差大小與某種子發芽多少之間的關系,現在從4月份的30天中隨機挑選了5天進行研究,且分別記錄了每天晝夜溫差與每天每100顆種子浸泡后的發芽數,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
溫差x/℃ | 10 | 11 | 13 | 12 | 8 |
發芽數y/顆 | 23 | 25 | 30 | 26 | 16 |
(1)從這5天中任選2天,記發芽的種子數分別為![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2) 若由線性回歸方程得到的估計數據與4月份所選5天的檢驗數據的誤差均不超過2顆,則認為得到的線性回歸方程是可靠的. 請根據4月7日,4月15日與4月21日這三天的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并判定所得的線性回歸方程是否可靠?
,并判定所得的線性回歸方程是否可靠?
參考公式:  ,
, ![]()
參考數據: ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知各項均為正數的數列![]() 的首項
的首項![]() ,
, ![]() 是數列
是數列![]() 的前
的前![]() 項和,且滿足:
項和,且滿足:
![]() .
.
(1)若![]() 成等比數列,求實數
成等比數列,求實數![]() 的值;
的值;
(2)若![]() ,求證:數列
,求證:數列 為等差數列;
為等差數列;
(3)在(2)的條件下,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A、B、C是△ABC的三個內角,則在下列各結論中,不正確的為( )
A. sin2A=sin2B+sin2C+2sinBsinCcos(B+C)
B. sin2B=sin2A+sin2C+2sinAsinCcos(A+C)
C. sin2C=sin2A+sin2B-2sinAsinBcosC
D. sin2(A+B)=sin2A+sin2B-2sinBsinCcos(A+B)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() (a>b>0)如圖,已知橢圓C:的左、右焦點分別為F1、F2 , 離心率為
(a>b>0)如圖,已知橢圓C:的左、右焦點分別為F1、F2 , 離心率為 ![]() ,點A是橢圓上任一點,△AF1F2的周長為
,點A是橢圓上任一點,△AF1F2的周長為 ![]() . (Ⅰ)求橢圓C的方程;
. (Ⅰ)求橢圓C的方程;
(Ⅱ)過點Q(﹣4,0)任作一動直線l交橢圓C于M,N兩點,記 ![]() ,若在線段MN上取一點R,使得
,若在線段MN上取一點R,使得 ![]() ,則當直線l轉動時,點R在某一定直線上運動,求該定直線的方程.
,則當直線l轉動時,點R在某一定直線上運動,求該定直線的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分13分)
已知圓滿足:
① 截y軸所得弦長為2;
②被x軸分成兩段圓弧,其弧長的比為3:1;
③圓心到直線l:x-2y=0的距離為![]() ,求該圓的方程.
,求該圓的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com