
【題目】已知橢圓![]() 的中心在坐標原點,左、右焦點
的中心在坐標原點,左、右焦點![]() 分別在
分別在![]() 軸上,離心率為
軸上,離心率為![]() ,在其上有一動點
,在其上有一動點![]() ,
,![]() 到點
到點![]() 距離的最小值是1.過
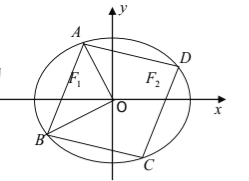
距離的最小值是1.過![]() 作一個平行四邊形,頂點
作一個平行四邊形,頂點![]() 都在橢圓
都在橢圓![]() 上,如圖所示.
上,如圖所示.

(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)判斷![]() 能否為菱形,并說明理由.
能否為菱形,并說明理由.
(Ⅲ)當![]() 的面積取到最大值時,判斷
的面積取到最大值時,判斷![]() 的形狀,并求出其最大值.
的形狀,并求出其最大值.
【答案】(I)![]() ;(II)不能,理由見解析;(III)矩形,且最大值為
;(II)不能,理由見解析;(III)矩形,且最大值為![]() .
.
【解析】
試題分析:(I)依題意有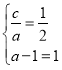 ,解得
,解得![]() ,所以橢圓方程為
,所以橢圓方程為![]() ;(II)令直線
;(II)令直線![]() 的方程為
的方程為![]() ,
,![]() ,聯立直線的方程和橢圓方程,利用根與系數關系,計算
,聯立直線的方程和橢圓方程,利用根與系數關系,計算![]() ,此方程無實數解,故
,此方程無實數解,故![]() 不成立,所以不存在菱形;(III)由題
不成立,所以不存在菱形;(III)由題![]() ,而
,而![]() ,由(2)根與系數關系可求得面積的表達式,再利用基本不等式計算得面積的最大值為
,由(2)根與系數關系可求得面積的表達式,再利用基本不等式計算得面積的最大值為![]() ,此時四邊形為矩形.
,此時四邊形為矩形.
試題解析:
(Ⅰ)依題,令橢圓![]() 的方程為
的方程為![]()
![]() ,
,
所以離心率![]() ,即
,即![]() .
.
令點![]() 的坐標為
的坐標為![]() ,所以
,所以![]() ,焦點
,焦點![]() ,即
,即![]()
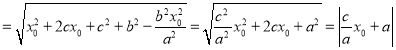 ,(沒有此步,不扣分)
,(沒有此步,不扣分)
因為![]() ,所以當
,所以當![]() 時,
時,![]() ,
,
由題![]() ,結合上述可知
,結合上述可知![]() ,所以
,所以![]() ,
,
于是橢圓![]() 的方程為
的方程為![]() .
.
(Ⅱ)由(Ⅰ)知![]() ,如圖,直線
,如圖,直線![]() 不能平行于
不能平行于![]() 軸,所以令直線的方程為
軸,所以令直線的方程為![]() ,
,![]()
聯立方程,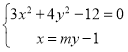 ,
,
得![]() ,
,
所以,![]() .
.
若![]() 是菱形,則
是菱形,則![]() ,即
,即![]() ,于是有
,于是有![]() ,
,
又![]() ,
,
所以有![]() ,
,
得到![]() ,可見
,可見![]() 沒有實數根,故
沒有實數根,故![]() 不能是菱形.
不能是菱形.
(Ⅲ)由題![]() ,而
,而![]() ,又
,又![]()
即![]() ,
,
由(Ⅱ)知![]() .
.
所以,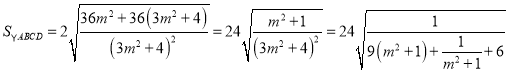 ,
,
因為函數![]() ,在
,在![]() 時,
時,![]() ,
,
即![]() 得最大值為6,此時
得最大值為6,此時![]() ,也就是
,也就是![]() 時,
時,
這時直線![]() 軸,可以判斷
軸,可以判斷![]() 是矩形.
是矩形.


科目:高中數學 來源: 題型:
【題目】 “中國式過馬路”是網友對部分中國人集體闖紅燈現象的一種調侃,即“湊夠一撮人就可以走了,和紅綠燈無關.”出現這種現象是大家受法不責眾的“從眾”心理影響,從而不顧及交通安全.某校對全校學生過馬路方式進行調查,在所有參與調查的人中,“跟從別人闖紅燈”“從不闖紅燈”“帶頭闖紅燈”人數如表所示:
跟從別人闖紅燈 | 從不闖紅燈 | 帶頭闖紅燈 | |
男生 | 800 | 450 | 200 |
女生 | 100 | 150 | 300 |
(Ⅰ)在所有參與調查的人中,用分層抽樣的方法抽取n人,已知“跟從別人闖紅燈”的人抽取了45 人,求n的值;
(Ⅱ)在“帶頭闖紅燈”的人中,將男生的200人編號為1,2,…,200;將女生的300人編號為201,202,…,500,用系統抽樣的方法抽取4人參加“文明交通”宣傳活動,若抽取的第一個人的編號為100,把抽取的4人看成一個總體,從這4人中任選取2人,求這兩人均是女生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 為奇
為奇
函數,且相鄰兩對稱軸間的距離為![]() .
.
(Ⅰ)當![]() 時,求
時,求![]() 的單調遞減區間;
的單調遞減區間;
(Ⅱ)將函數![]() 的圖象沿
的圖象沿![]() 軸方向向右平移
軸方向向右平移![]() 個單位長度,再把橫坐標縮短到原來的
個單位長度,再把橫坐標縮短到原來的![]() (縱坐標不變),
(縱坐標不變),
得到函數![]() 的圖象.當
的圖象.當![]() 時,求函數
時,求函數![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學餐飲中心為了了解新生的飲食習慣,利用簡單隨機抽樣的方法在全校一年級學生中進行了抽樣調查,調查結果如下表所示:
喜歡甜品 | 不喜歡甜品 | 合計 | |
南方學生 | 60 | 20 | 80 |
北方學生 | 10 | 10 | 20 |
合計 | 70 | 30 | 100 |
(1)根據表中數據,問是否有95%的把握認為“南方學生和北方學生在選用甜品的飲食習慣方面有差異”;
(2)根據(1)的結論,你能否提出更好的調查方法來了解該校大學新生的飲食習慣,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,游客從某旅游景區的景點![]() 處下上至
處下上至![]() 處有兩種路徑.一種是從
處有兩種路徑.一種是從![]() 沿直線步行到
沿直線步行到![]() ,另一種是先從
,另一種是先從![]() 沿索道乘纜車到
沿索道乘纜車到![]() ,然后從
,然后從![]() 沿直線步行到
沿直線步行到![]() .現有甲、乙兩位游客從
.現有甲、乙兩位游客從![]() 處下山,甲沿
處下山,甲沿![]() 勻速步行,速度為
勻速步行,速度為![]() .在甲出發
.在甲出發![]() 后,乙從
后,乙從![]() 乘纜車到
乘纜車到![]() ,在
,在![]() 處停留
處停留![]() 后,再從
后,再從![]() 勻速步行到
勻速步行到![]() ,假設纜車勻速直線運動的速度為
,假設纜車勻速直線運動的速度為![]() ,山路
,山路![]() 長為1260
長為1260![]() ,經測量
,經測量![]() ,
,![]() .
.

(1)求索道![]() 的長;
的長;
(2)問:乙出發多少![]() 后,乙在纜車上與甲的距離最短?
后,乙在纜車上與甲的距離最短?
(3)為使兩位游客在![]() 處互相等待的時間不超過
處互相等待的時間不超過![]() ,乙步行的速度應控制在什么范圍內?
,乙步行的速度應控制在什么范圍內?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com