【題目】已知函數(shù)
.
（1）若
.證明函數(shù)
有且僅有兩個零點；
（2）若函數(shù)存在兩個零點
，證明：
.
【答案】（1）證明見解析；（2）證明見解析.
【解析】
（1）當
時，函數(shù)
，定義域為
，利用導數(shù)分析其單調(diào)性
，使
在
單調(diào)遞減，在
單調(diào)遞增，進而分別計算并判斷
，
，
與零的大小比較，最后由零點的存在性定理即可確定零點的個數(shù)；
（2）由
是函數(shù)的兩個零點，知
，進而表示
，再由分析法逐步反推不等式，最后令
，構(gòu)造函數(shù)
，由（1）的單調(diào)性分析，表示最小值并由雙勾函數(shù)證得
，即可得證.
（1）由題可知，定義域
當時，函數(shù)，則
，
（
為
的導函數(shù)）
單調(diào)遞增
，
使
.
時，
單調(diào)遞減；
時，
單調(diào)遞增
所以
由雙勾函數(shù)性質(zhì)可知，在
遞減，
，
，且
，
在上有且只有一個零點
又
，且
所以在上有且只有一個零點
綜上，函數(shù)有且僅有兩個零點
（2）由是函數(shù)的兩個零點，知
要證
需證
令
需證
令
與（1）同理得
所以
故
天天向上一本好卷系列答案
小學生10分鐘應(yīng)用題系列答案科目：高中數(shù)學 來源： 題型：
【題目】多面體歐拉定理是指對于簡單多面體，其各維對象數(shù)總滿足一定的數(shù)量關(guān)系，在三維空間中，多面體歐拉定理可表示為：頂點數(shù)＋表面數(shù)－棱長數(shù)＝2.在數(shù)學上，富勒烯的結(jié)構(gòu)都是以正五邊形和正六邊形面組成的凸多面體，例如富勒烯
（結(jié)構(gòu)圖如圖）是單純用碳原子組成的穩(wěn)定分子，具有60個頂點和32個面，其中12個為正五邊形，20個為正六邊形.除外具有封閉籠狀結(jié)構(gòu)的富勒烯還可能有
，
，
，
，
，
，
，等，則結(jié)構(gòu)含有正六邊形的個數(shù)為（ ）
A.12B.24C.30D.32
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某城市對一項惠民市政工程滿意程度（分值：
分）進行網(wǎng)上調(diào)查，有2000位市民參加了投票，經(jīng)統(tǒng)計，得到如下頻率分布直方圖（部分圖）：
現(xiàn)用分層抽樣的方法從所有參與網(wǎng)上投票的市民中隨機抽取
位市民召開座談會，其中滿意程度在
的有5人．
（1）求的值，并填寫下表（2000位參與投票分數(shù)和人數(shù)分布統(tǒng)計）；
滿意程度（分數(shù)） |
|
|
|
|
|
人數(shù) |
（2）求市民投票滿意程度的平均分（各分數(shù)段取中點值）；
（3）若滿意程度在的5人中恰有2位為女性，座談會將從這5位市民中任選兩位發(fā)言，求男性甲或女性乙被選中的概率．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】(2017·衢州調(diào)研)已知四棱錐P－ABCD的底面ABCD是菱形，∠ADC＝120°，AD的中點M是頂點P在底面ABCD的射影，N是PC的中點.
(1)求證：平面MPB⊥平面PBC；
(2)若MP＝MC，求直線BN與平面PMC所成角的正弦值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】2020年寒假，因為“新冠”疫情全體學生只能在家進行網(wǎng)上學習，為了研究學生網(wǎng)上學習的情況，某學校隨機抽取
名學生對線上教學進行調(diào)查，其中男生與女生的人數(shù)之比為
，抽取的學生中男生有
人對線上教學滿意，女生中有
名表示對線上教學不滿意.
（1）完成
列聯(lián)表，并回答能否有
的把握認為“對線上教學是否滿意 與性別有關(guān)”；
態(tài)度 性別 | 滿意 | 不滿意 | 合計 |
男生 | |||
女生 | |||
合計 | 100 |
（2）從被調(diào)查的對線上教學滿意的學生中，利用分層抽樣抽取
名學生，再在這名學生中抽取
名學生，作線上學習的經(jīng)驗介紹，求其中抽取一名男生與一名女生的概率.
附：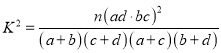
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，在三棱錐
中，
是邊長為2的正三角形，
是等腰直角三角形，
.
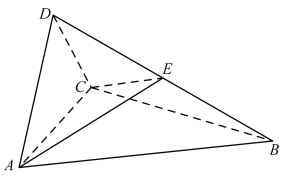
（I）證明：平面
平面ABC；
（II）點E在BD上，若平面ACE把三棱錐分成體積相等的兩部分，求二面角
的余弦值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知點（1，e），（e，
）在橢圓上C：
1（a＞b＞0），其中e為橢圓的離心率.
（1）求橢圓C的方程；
（2）直線l經(jīng)過C的上頂點且l與拋物線M：y2＝4x交于P，Q兩點，F為橢圓的左焦點，直線FP，FQ與M分別交于點D（異于點P），E（異于點Q），證明：直線DE的斜率為定值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
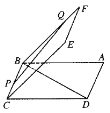
【題目】如圖，正方形
與正方形
所成角的二面角的平面角的大小是
是正方形所在平面內(nèi)的一條動直線，則直線
與
所成角的取值范圍是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某高校設(shè)計了一個實驗學科的實驗考查方案：考生從6道備選題中一次性隨機抽取3題，按照題目要求獨立完成全部實驗操作．規(guī)定：至少正確完成其中2題的便可提交通過．已知6道備選題中考生甲有4道題能正確完成，2道題不能完成．
（1）求出甲考生正確完成題數(shù)的概率分布列，并計算數(shù)學期望；
（2）若考生乙每題正確完成的概率都是
，且每題正確完成與否互不影響．試從至少正確完成2題的概率分析比較兩位考生的實驗操作能力．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
