
【題目】已知直線l:y=kx+1(k≠0)與橢圓3x2+y2=a相交于A、B兩個不同的點,記l與y軸的交點為C.
(Ⅰ)若k=1,且|AB|= ![]() ,求實數a的值;
,求實數a的值;
(Ⅱ)若 ![]() =2
=2 ![]() ,求△AOB面積的最大值,及此時橢圓的方程.
,求△AOB面積的最大值,及此時橢圓的方程.
【答案】解:設A(x1,y1),B(x2,y2),
(Ⅰ)由 ![]() 得4x2+2x+1﹣a=0,
得4x2+2x+1﹣a=0,
則x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
則|AB|= ![]() =
= ![]() ,解得a=2.
,解得a=2.
(Ⅱ)由 ![]() ,得(3+k2)x2+2kx+1﹣a=0,
,得(3+k2)x2+2kx+1﹣a=0,
則x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
由 ![]() =2
=2 ![]() 得(﹣x1,1﹣y1)=2(x2,y2﹣1),
得(﹣x1,1﹣y1)=2(x2,y2﹣1),
解得x1=﹣2x2,代入上式得:
x1+x2=﹣x2=﹣ ![]() ,則x2=
,則x2= ![]() ,
,
![]() =
= ![]() =
= ![]() ,
,
當且僅當k2=3時取等號,此時x2= ![]() ,x1x2=﹣2x22=﹣2×
,x1x2=﹣2x22=﹣2× ![]() ,
,
又x1x2= ![]() =
= ![]() ,
,
則 ![]() =﹣
=﹣ ![]() ,解得a=5.
,解得a=5.
所以,△AOB面積的最大值為 ![]() ,此時橢圓的方程為3x2+y2=5
,此時橢圓的方程為3x2+y2=5
【解析】(1)本小題的關鍵是線段AB長的表示,求得過程為![]() ;(2)本題關鍵在于三角形AOB面積的表示,求得過程為:S△AOB=
;(2)本題關鍵在于三角形AOB面積的表示,求得過程為:S△AOB=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知某射擊運動員每次擊中目標的概率都是0.7.現采用隨機模擬的方法估計該運動員射擊4次,至少擊中2次的概率:先由計算器算出0~9之間取整數值的隨機數,指定0,1,2表示沒有擊中目標,3,4,5,6,7,8,9表示擊中目標;因為射擊4次,故以每4個隨機數為一組,代表射擊4次的結果.經隨機模擬產生了20組隨機數:
5727 0293 7140 9857 0347
4373 8636 9647 1417 4698
0371 6233 2616 8045 6011
3661 9597 7424 6710 4281
據此估計,該射擊運動員射擊4次至少擊中2次的概率為( )
A. 0.8 B. 0.85 C. 0.9 D. 0.95
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下四個關于圓錐曲線的命題中:
①雙曲線 ![]() 與橢圓
與橢圓 ![]() 有相同的焦點;
有相同的焦點;
②以拋物線的焦點弦(過焦點的直線截拋物線所得的線段)為直徑的圓與拋物線的準線是相切的;
③設A、B為兩個定點,k為常數,若|PA|﹣|PB|=k,則動點P的軌跡為雙曲線;
④過定圓C上一點A作圓的動弦AB,O為原點,若 ![]() 則動點P的軌跡為橢圓.其中正確的個數是( )
則動點P的軌跡為橢圓.其中正確的個數是( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某個體服裝店經營某種服裝,在某周內獲得的純利潤y(單位:元)與該周每天銷售這種服裝的件數x之間的一組數據關系如下表:
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
(1)求純利潤y與每天銷售件數x之間的回歸方程;
(2)若該周內某天銷售服裝20件,估計可獲得純利潤多少元?
已知:![]() =280,
=280,![]() xiyi=3 487,
xiyi=3 487,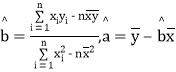 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直線l1 , l2分別過點A(3 ![]() ,2),B(
,2),B( ![]() ,6),它們分別繞點A,B旋轉,但始終保持l1⊥l2 . 若l1與l2的交點為P,坐標原點為O,則線段OP長度的取值范圍是( )
,6),它們分別繞點A,B旋轉,但始終保持l1⊥l2 . 若l1與l2的交點為P,坐標原點為O,則線段OP長度的取值范圍是( )
A.[3,9]
B.[3,6]
C.[6,9]
D.[9,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三點A(1,2),B(﹣3,0),C(3,﹣2).
(1)求證△ABC為等腰直角三角形;
(2)若直線3x﹣y=0上存在一點P,使得△PAC面積與△PAB面積相等,求點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知p:x2﹣2x﹣8≤0,q:x2+mx﹣6m2≤0,m>0.
(1)若q是p的必要不充分條件,求m的取值范圍;
(2)若p是q的充分不必要條件,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】廠為了對新研發的一種產品進行合理定價,將該產品按事先擬定的價格進行試銷,得到如下數據:
單價x/元 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量y/件 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求線性回歸方程![]() =
=![]() x+
x+![]() ,其中
,其中![]() =-20,
=-20, ![]() =
=![]() -
-![]()
![]() .
.
(2)預計在今后的銷售中,銷量與單價仍然服從(1)中的關系,且該產品的成本是4元/件,為使工廠獲得最大利潤,該產品的單價應定為多少元?(利潤=銷售收入-成本)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com