Question

【題目】已知梯形ABCD中，AD∥BC，∠ABC =∠BAD =，AB=BC=2AD=4，E、F分別是AB、CD上的點，EF∥BC，AE = ，G是BC的中點。沿EF將梯形ABCD翻折，使平面AEFD⊥平面EBCF．

（1）若以F、B、C、D為頂點的三棱錐的體積記為，求的最大值；

（2）當(dāng) 取得最大值時，求二面角D-BF-C的余弦值．

Answer 1

【答案】(1) 有最大值為;(2) 二面角的余弦值為：－.

【解析】試題分析：（1）由平面， ，可得，進(jìn)而由面面垂直的性質(zhì)定理得到平面，進(jìn)而建立空間坐標(biāo)系，可得的解析式，根據(jù)二次函數(shù)的性質(zhì)，易求出有最大值；（2）根據(jù)（1）的結(jié)論平面的一個法向量為，利用向量垂直數(shù)量積為零列方程組求出平面的法向量，代入向量夾角公式即可得到二面角的余弦值.

試題解析：（1）∵平面平面,AE⊥EF,

∴AE⊥面平面,AE⊥EF,AE⊥BE,又BE⊥EF,故可如圖建立空間坐標(biāo)系E-xyz．則A（0，0，2），B（2，0，0），G（2，2，0），D（0，2，2），

E（0，0，0）∵AD∥面BFC，

所以VA-BFC＝

，即時有最大值為．

（2）設(shè)平面DBF的法向量為，∵AE=2, B（2，0，0），

D（0，2，2），F(xiàn)（0，3，0）,∴ （－2，2，2）,

則，即，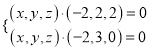

取x＝3，則y＝2，z＝1，∴

面BCF的一個法向量為

則cos<>=.

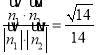由于所求二面角D-BF-C的平面角為鈍角，所以此二面角的余弦值為：－