
【題目】成等差數列的三個正數的和等于15,并且這三個數分別加上2、5、13后成為等比數列{bn}中的b3、b4、b5.
(Ⅰ)求數列{bn}的通項公式;
(Ⅱ)數列{bn}的前n項和為Sn,求證:數列{Sn+![]() }是等比數列.
}是等比數列.
【答案】(Ⅰ)![]() (Ⅱ)詳見解析
(Ⅱ)詳見解析
【解析】
試題分析:(I)利用成等差數列的三個正數的和等于15可設三個數分別為5-d,5,5+d,代入等比數列中可求d,進一步可求數列{bn}的通項公式;(II)根據(I)及等比數列的前 n項和公式可求![]() ,要證數列
,要證數列![]() 是等比數列
是等比數列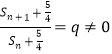 即可
即可
試題解析:(I)設成等差數列的三個正數分別為a﹣d,a,a+d
依題意,得a﹣d+a+a+d=15,解得a=5
所以{bn}中的依次為7﹣d,10,18+d
依題意,有(7﹣d)(18+d)=100,解得d=2或d=﹣13(舍去)
故{bn}的第3項為5,公比為2
由b3=b122,即5=4b1,解得![]()
所以{bn}是以![]() 首項,2為公比的等比數列,通項公式為
首項,2為公比的等比數列,通項公式為![]() ……………6分
……………6分
(II)數列{bn}的前和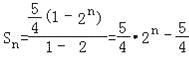
即![]() ,所以
,所以![]() ,
,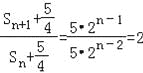
因此{![]() }是以
}是以![]() 為首項,公比為2的等比數列 …………………12分
為首項,公比為2的等比數列 …………………12分


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,左頂點為
,左頂點為![]() ,過原點且斜率不為0的直線與橢圓交于
,過原點且斜率不為0的直線與橢圓交于![]() 兩點,其中點
兩點,其中點![]() 在第二象限,過點
在第二象限,過點![]() 作
作![]() 軸的垂線交
軸的垂線交![]() 于點
于點![]() .
.

⑴求橢圓的標準方程;
⑵當直線![]() 的斜率為
的斜率為![]() 時,求
時,求![]() 的面積;
的面積;
⑶試比較![]() 與
與![]() 大小.
大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,以坐標原點O為圓心的單位圓與x軸正半軸相交于點A,點B,P在單位圓上,且![]()
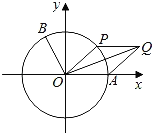
(1)求![]() 的值;
的值;
(2)設![]()
![]() ,四邊形
,四邊形![]() 的面積為
的面積為![]() ,
,![]() ,求
,求![]() 的最值及此時
的最值及此時![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記U={1,2,…,100},對數列{an}(n∈N*)和U的子集T,若T=,定義ST=0;若T={t1 , t2 , …,tk},定義ST= ![]() +
+ ![]() +…+
+…+ ![]() .例如:T={1,3,66}時,ST=a1+a3+a66 . 現設{an}(n∈N*)是公比為3的等比數列,且當T={2,4}時,ST=30.
.例如:T={1,3,66}時,ST=a1+a3+a66 . 現設{an}(n∈N*)是公比為3的等比數列,且當T={2,4}時,ST=30.
(1)求數列{an}的通項公式;
(2)對任意正整數k(1≤k≤100),若T{1,2,…,k},求證:ST<ak+1;
(3)設CU,DU,SC≥SD , 求證:SC+SC∩D≥2SD .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓 ![]() 1(a>
1(a> ![]() )的右焦點為F,右頂點為A,已知
)的右焦點為F,右頂點為A,已知 ![]() ,其中O為原點,e為橢圓的離心率.
,其中O為原點,e為橢圓的離心率.
(1)求橢圓的方程;
(2)設過點A的直線l與橢圓交于B(B不在x軸上),垂直于l的直線與l交于點M,與y軸交于點H,若BF⊥HF,且∠MOA=∠MAO,求直線l的斜率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com