
已知函數(shù) .
.
(I)若a=-1,求函數(shù) 的單調區(qū)間;
的單調區(qū)間;
(Ⅱ)若函數(shù) 的圖象在點(2,f(2))處的切線的傾斜角為45o,對于任意的t
的圖象在點(2,f(2))處的切線的傾斜角為45o,對于任意的t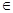 [1,2],函數(shù)
[1,2],函數(shù) 是
是 的導函數(shù))在區(qū)間(t,3)上總不是單調函數(shù),求m的取值范圍;
的導函數(shù))在區(qū)間(t,3)上總不是單調函數(shù),求m的取值范圍;
(Ⅲ)求證:
(1) 的單調增區(qū)間為
的單調增區(qū)間為 ,減區(qū)間為
,減區(qū)間為 .
.
(2)
(3)由(Ⅰ)可知當 時
時 ,即
,即 根據(jù)函數(shù)最值來證明即可。
根據(jù)函數(shù)最值來證明即可。
【解析】
試題分析:解:(Ⅰ)當 時,
時, 解
解 得
得 ;解
;解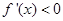 得
得
 的單調增區(qū)間為
的單調增區(qū)間為 ,減區(qū)間為
,減區(qū)間為 . ………4分
. ………4分
(Ⅱ) ∵ ∴
∴ 得
得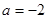 ,
,
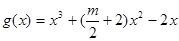 ,∴
,∴
∵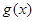 在區(qū)間
在區(qū)間 上總不是單調函數(shù),且
上總不是單調函數(shù),且 ∴
∴ 7分
7分
由題意知:對于任意的 ,
,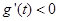 恒成立,
恒成立,
所以, ,∴
,∴ .
.
(Ⅲ)證明如下: 由(Ⅰ)可知
當 時
時 ,即
,即 ,
,
∴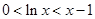 對一切
對一切 成立. 10分
成立. 10分
∵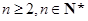 ,則有
,則有 ,∴
,∴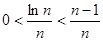 . 11分
. 11分
 .
13分
.
13分
考點:導數(shù)的運用
點評:主要是考查了導數(shù)在研究函數(shù)單調性的運用,屬于中檔題。


科目:高中數(shù)學 來源: 題型:
(本小題共14分)
已知函數(shù)![]()
![]()
(I)若![]() ,求函數(shù)
,求函數(shù)![]() 的解析式;
的解析式;
(II)若![]() ,且
,且![]() 在區(qū)間
在區(qū)間![]() 上單調遞增,求實數(shù)
上單調遞增,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源:2011年河北省石家莊市高三第一次模擬考試數(shù)學試卷文科 題型:解答題
已知函數(shù)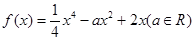 .
.
(I)若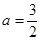 ,求函數(shù)
,求函數(shù) 極值;ww..com
極值;ww..com
(II)設F(x)= ,若函數(shù)F(x)在[0,1]上單調遞增,求
,若函數(shù)F(x)在[0,1]上單調遞增,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源:2010年新課標版廣東省遂溪縣高一數(shù)學必修一(函數(shù)、導數(shù)、方程與不等式)單元測試 題型:解答題
已知函數(shù) .
.
(I)若函數(shù) 在點
在點 處的切線斜率為4,求實數(shù)
處的切線斜率為4,求實數(shù) 的值;
的值;
(II)若函數(shù) 在區(qū)間
在區(qū)間 上存在零點,求實數(shù)
上存在零點,求實數(shù) 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數(shù)學 來源:2010年大連市高三高考壓軸考試理科數(shù)學卷 題型:解答題
已知函數(shù)
(I)
如 ,求
,求 的單調區(qū)間;
的單調區(qū)間;
(II) 若 在
在 單調增加,在
單調增加,在 單調減少,
單調減少,
證明 <6.
<6.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com