
【題目】某中學為了組建一支業余足球隊,在高一年級隨機選取50名男生測量身高,發現被測男生的身高全部在![]() 到
到![]() 之間,將測量結果按如下方式分成六組:第1組
之間,將測量結果按如下方式分成六組:第1組![]() ,第2組
,第2組![]() ,…,第6組
,…,第6組![]() ,如圖是按上述分組得到的頻率分布直方圖,以頻率近似概率.
,如圖是按上述分組得到的頻率分布直方圖,以頻率近似概率.
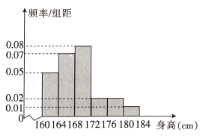
(1)若學校要從中選1名男生擔任足球隊長,求被選取的男生恰好在第5組或第6組的概率;
(2)試估計該校高一年級全體男生身高的平均數(同一組中的數據用該組區間的中點值代表)與中位數;
(3)現在從第5與第6組男生中選取兩名同學擔任守門員,求選取的兩人中最多有1名男生來自第5組的概率.
【答案】(1)0.12;(2)平均數為168.72,中位數為168.25;(3)![]() .
.
【解析】
(1)由直方圖可得,被選取的男生恰好在第5組或第6組的概率![]() ;(2)每個矩形的中點橫坐標與該矩形的縱坐標、組距相乘后求和可得平均值;直方圖左右兩邊面積相等處橫坐標表示中位數;(3)利用列舉法,從第5與第6組男生中選取兩名同學擔任守門員共有15種情況,其中選取的兩人中最多有1名男生來自第5組的情況有9種,由古典概型概率公式可得結果.
;(2)每個矩形的中點橫坐標與該矩形的縱坐標、組距相乘后求和可得平均值;直方圖左右兩邊面積相等處橫坐標表示中位數;(3)利用列舉法,從第5與第6組男生中選取兩名同學擔任守門員共有15種情況,其中選取的兩人中最多有1名男生來自第5組的情況有9種,由古典概型概率公式可得結果.
(1)被選取的男生恰好在第5組或第6組的概率
![]() .
.
(2)全體男生身高的平均數為![]()
![]() .
.
設全體男生身高的中位數為![]() ,因為第1組
,因為第1組![]() 對應的頻率為0.20,第2組
對應的頻率為0.20,第2組![]() 對應的頻率為0.28,所以
對應的頻率為0.28,所以![]() ,則
,則![]() ,解得
,解得![]() .
.
(3)第5組有![]() 人,記為
人,記為![]() ,
,![]() ,
,![]() ,
,![]() ,同理第6組有2人記為
,同理第6組有2人記為![]() ,
,![]() ,
,
所有的情況為![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,共15種,
,共15種,
選取的兩人中最多有1名男生來自第5組的有![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共9種,
共9種,
所以所求概率為![]() .
.


科目:高中數學 來源: 題型:
【題目】正方形![]() 沿對角線
沿對角線![]() 折成直二面角,下列結論:①異面直線
折成直二面角,下列結論:①異面直線![]() 與
與![]() 所成的角為
所成的角為![]() ;②
;②![]() ;③
;③![]() 是等邊三角形;④二面角
是等邊三角形;④二面角![]() 的平面角正切值是
的平面角正切值是![]() ;其中正確結論是______.(寫出你認為正確的所有結論的序號)
;其中正確結論是______.(寫出你認為正確的所有結論的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校在平面圖為矩形的操場ABCD內進行體操表演,其中AB=40,BC=15,O為AB上一點,且BO=10,線段OC、OD、MN為表演隊列所在位置(M、N分別在線段OD、OC上),△OCD內的點P為領隊位置,且P到OC、OD的距離分別為![]() 、
、![]() ,記OM=d,我們知道當△OMN面積最小時觀賞效果最好.
,記OM=d,我們知道當△OMN面積最小時觀賞效果最好.
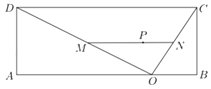
(1)當d為何值時,P為隊列MN的中點;
(2)怎樣安排M的位置才能使觀賞效果最好?求出此時△OMN的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電子商務平臺的管理員隨機抽取了1000位上網購物者,并對其年齡(在10歲到69歲之間)進行了調查,統計情況如下表所示.
年齡 |
|
|
|
|
|
|
人數 | 100 | 150 |
| 200 |
| 50 |
已知![]() ,
,![]() ,
,![]() 三個年齡段的上網購物的人數依次構成遞減的等比數列.
三個年齡段的上網購物的人數依次構成遞減的等比數列.
(1)求![]() 的值;
的值;
(2)若將年齡在![]() 內的上網購物者定義為“消費主力軍”,其他年齡段內的上網購物者定義為“消費潛力軍”.現采用分層抽樣的方式從參與調查的1000位上網購物者中抽取5人,再從這5人中抽取2人,求這2人中至少有一人是消費潛力軍的概率.
內的上網購物者定義為“消費主力軍”,其他年齡段內的上網購物者定義為“消費潛力軍”.現采用分層抽樣的方式從參與調查的1000位上網購物者中抽取5人,再從這5人中抽取2人,求這2人中至少有一人是消費潛力軍的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中, ![]() 是正方形,
是正方形, ![]() 平面
平面![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別是
分別是 ![]() ,
, ![]() ,
, ![]() 的中點.
的中點.
(1)求證:平面![]() 平面
平面![]() .
.
(2)在線段![]() 上確定一點
上確定一點![]() ,使
,使![]() 平面
平面![]() ,并給出證明.
,并給出證明.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司有4家直營店![]() ,
, ![]() ,
, ![]() ,
, ![]() ,現需將6箱貨物運送至直營店進行銷售,各直營店出售該貨物以往所得利潤統計如下表所示.根據此表,該公司獲得最大總利潤的運送方式有
,現需將6箱貨物運送至直營店進行銷售,各直營店出售該貨物以往所得利潤統計如下表所示.根據此表,該公司獲得最大總利潤的運送方式有

A. ![]() 種 B.
種 B. ![]() 種 C.
種 C. ![]() 種 D.
種 D. ![]() 種
種
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com