設等差數列{an}的前n項和為Sn. 若a1＝－11，a4＋a6＝－6，則當Sn取最小值時，n等于( )
| A．6 | B．7 | C．8 | D．9 |
A
解析試題分析：根據等差數列的性質化簡a4+a6=-6，得到a5的值，然后根據a1的值，利用等差數列的通項公式即可求出公差d的值，根據a1和d的值寫出等差數列的通項公式，進而寫出等差數列的前n項和公式Sn，配方后即可得到Sn取最小值時n的值．解：由a4+a6=2a5=-6，解得a5=-3，又a1=-11，所以a5=a1+4d=-11+4d=-3，解得d=2，則an=-11+2（n-1）=2n-13，所以Sn=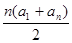
=n2-12n=（n-6）2-36，所以當n=6時，Sn取最小值．故答案為A
考點：等差數列的通項公式及前n項和公式
點評：此題考查學生靈活運用等差數列的通項公式及前n項和公式化簡求值，掌握等差數列的性質，是一道基礎題
科目：高中數學 來源： 題型：單選題
數列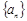
中，如果
＝
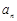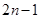(n＝1，2，3，…) ，那么這個數列是( )．
| A．公差為2的等差數列 | B．公差為-2的等差數列 |
| C．首項為-3的等差數列 | D．首項為-3的等比數列 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的前
項和為
.若
是
的等比中項, 
,則
=（ ）. 
為等差數列
的前
項和，
，則
=（ ）
中，
，
，則
=
的前
項和為
.若
是
的等比中項, 
,則
等于（）
中，
=1，
，則
的值為 （ ）
的前n項和為
,若
,
,則當
=（ ）
為等差數列，公差
，
為其前
項和，若
，則
=
