
【題目】已知關于x的不等式ax2+(1﹣a)x﹣1>0
(1)當a=2時,求不等式的解集.
(2)當a>﹣1時.求不等式的解集.
【答案】
(1)解:原不等式即(x﹣1)(ax+1)>0,當a=2時,即(x﹣1)(2x+1)>0,
求得x<﹣ ![]() ,或x>1,故不等式的解集為{x|x<﹣
,或x>1,故不等式的解集為{x|x<﹣ ![]() ,或x>1}
,或x>1}
(2)解:二次項系數含有參數,因此對a在0點處分開討論.
若a≠0,則原不等式ax2+(1﹣a)x﹣1>0等價于(x﹣1)(ax+1)>0.
其對應方程的根為﹣ ![]() 與1.
與1.
又因為a>﹣1,則①當a=0時,原不等式為x﹣1>0,
所以原不等式的解集為{x|x>1};
②當a>0時,﹣ ![]() <1,所以原不等式的解集為{x|x<﹣
<1,所以原不等式的解集為{x|x<﹣ ![]() ,或 x>1};
,或 x>1};
③當﹣1<a<0時,﹣ ![]() >1,所以原不等式的解集為{x|1<x<﹣
>1,所以原不等式的解集為{x|1<x<﹣ ![]() }
}
【解析】(1)當a=2時,不等式即即(x﹣1)(2x+1)>0,由此求得x的范圍.(2)不等式即(x﹣1)(ax+1)>0,其對應方程的根為﹣ ![]() 與1,利用二次函數的性質分類討論求得它的解集.
與1,利用二次函數的性質分類討論求得它的解集.


科目:高中數學 來源: 題型:
【題目】已知圓![]() 和點
和點![]() ,動圓
,動圓![]() 經過點
經過點![]() 且與圓
且與圓![]() 相切,圓心
相切,圓心![]() 的軌跡為曲線
的軌跡為曲線![]()
(1)求曲線![]() 的方程;
的方程;
(2)點![]() 是曲線
是曲線![]() 與
與![]() 軸正半軸的交點,點
軸正半軸的交點,點![]() 在曲線
在曲線![]() 上,若直線
上,若直線![]() 的斜率
的斜率![]() 滿足
滿足![]() 求
求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在極坐標系中,曲線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點
,以極點為原點![]() ,極軸為
,極軸為![]() 軸正半軸(兩坐標系取相同的單位長度)的直角坐標系
軸正半軸(兩坐標系取相同的單位長度)的直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為:
的參數方程為:![]() (
(![]() 為參數).
為參數).
(1)求曲線![]() 的直角坐標方程與曲線
的直角坐標方程與曲線![]() 的普通方程;
的普通方程;
(2)將曲線![]() 經過伸縮變換
經過伸縮變換 后得到曲線
后得到曲線![]() ,若
,若![]() 分別是曲線
分別是曲線![]() 和曲線
和曲線![]() 上的動點,求
上的動點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,網格紙上小正方形的邊長為![]() ,粗實線畫出的是某幾何體的三視圖,該幾何體由一平面將一圓柱截去一部分所得,則該幾何體的體積為( )
,粗實線畫出的是某幾何體的三視圖,該幾何體由一平面將一圓柱截去一部分所得,則該幾何體的體積為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}滿足a3=7,a5+a7=26.{an}的前n項和為Sn .
(1)求an及Sn;
(2)令bn=﹣ ![]() (n∈N*),求數列{bn}的前n項和Tn .
(n∈N*),求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年“雙節”期間,高速公路車輛較多.某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速![]() 分成六段:
分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如圖的頻率分布直方圖.
后得到如圖的頻率分布直方圖.
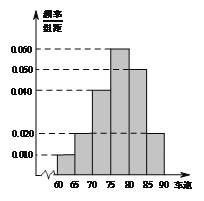
(I)某調查公司在采樣中,用到的是什么抽樣方法?
(II)求這40輛小型車輛車速的眾數、中位數及平均數的估計值;
(III)若從車速在![]() 的車輛中任抽取2輛,求車速在
的車輛中任抽取2輛,求車速在![]() 的車輛至少有一輛的概率.
的車輛至少有一輛的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】天氣預報說,在今后的三天中,每一天下雨的概率均為50%.現采用隨機模擬試驗的方法估計這三天中恰有兩天下雨的概率:先利用計算器產生0到9之間取整數值的隨機數,用0,1,2,3,4表示下雨,用5,6,7,8,9表示不下雨;再以每三個隨機數作為一組,代表這三天的下雨情況.經隨機模擬試驗產生了如下20組隨機數:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
據此估計,這三天中恰有兩天下雨的概率近似為( )
A. 0.30 B. 0.35 C. 0.40 D. 0.50
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學藝術專業400名學生參加某次測評,根據男女學生人數比例,使用分層抽樣的方法從中隨機抽取了100名學生,記錄他們的分數,將數據分成7組:[20,30),[30,40),┄,[80,90],并整理得到如下頻率分布直方圖:
(Ⅰ)從總體的400名學生中隨機抽取一人,估計其分數小于70的概率;
(Ⅱ)已知樣本中分數小于40的學生有5人,試估計總體中分數在區間[40,50)內的人數;
(Ⅲ)已知樣本中有一半男生的分數不小于70,且樣本中分數不小于70的男女生人數相等.試估計總體中男生和女生人數的比例.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com