
【題目】已知定義在![]() 上的奇函數(shù)
上的奇函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上是減函數(shù),且滿足
上是減函數(shù),且滿足![]() .令
.令![]() ,則
,則![]() 的大小關(guān)系為( )
的大小關(guān)系為( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】分析:分析函數(shù)可知函數(shù)是周期為4的函數(shù),且關(guān)于x =﹣1對(duì)稱,所以可得f(x)在[﹣1,1]上是增函數(shù),比較![]() ,
,![]() 的大小即可得解.
的大小即可得解.
詳解:∵奇函數(shù)f(x)在區(qū)間[﹣2,﹣1]上是減函數(shù),且滿足f(x﹣2)=﹣f(x).
∴f(x﹣4)=﹣f(x﹣2)=f(x),即函數(shù)的周期是4,
又f(x﹣2)=﹣f(x)=f(﹣x),
則函數(shù)關(guān)于x =﹣1對(duì)稱,
則函數(shù)在[﹣1,0]上是增函數(shù),且f(x)在[﹣1,1]上是增函數(shù),
![]() ,
,
![]() ,
,
![]() .
.
又![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() .
.
綜上![]() .即0<c<a<b<1,
.即0<c<a<b<1,
又f(x)在[﹣1,1]上是增函數(shù),
∴f(b)>f(a)>f(c),
故選:A.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知小李每次打靶命中靶心的概率都為40%,現(xiàn)采用隨機(jī)模擬的方法估計(jì)小李三次打靶恰有兩次命中靶心的概率.先由計(jì)算器產(chǎn)生0到9之間取整數(shù)值的隨機(jī)數(shù),指定0,1,2,3表示命中靶心,4,5,6,7,8,9表示未命中靶心,再以每三個(gè)隨機(jī)數(shù)為一組,代表三次打靶的結(jié)果,經(jīng)隨機(jī)模擬產(chǎn)生了如下20組隨機(jī)數(shù):
321 421 191 925 271 932 800 478
589 663 531 297 396 021 546 388
230 113 507 965
據(jù)此估計(jì),小李三次打靶恰有兩次命中的概率為( )
A. 0.25 B. 0.30
C. 0.35 D. 0.40
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商品近一個(gè)月內(nèi)(30天)預(yù)計(jì)日銷(xiāo)量![]() (件)與時(shí)間t(天)的關(guān)系如圖1所示,單價(jià)
(件)與時(shí)間t(天)的關(guān)系如圖1所示,單價(jià)![]() (萬(wàn)元/件)與時(shí)間t(天)的函數(shù)關(guān)系如圖2所示,(t為整數(shù))
(萬(wàn)元/件)與時(shí)間t(天)的函數(shù)關(guān)系如圖2所示,(t為整數(shù))
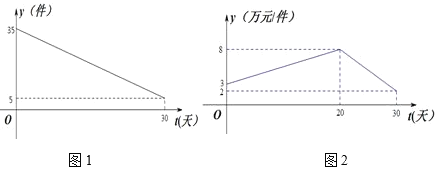
(1)試寫(xiě)出![]() 與
與![]() 的解析式;
的解析式;
(2)求此商品日銷(xiāo)售額的最大值?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=log4(4x+1)+kx(k∈R)是偶函數(shù).
(1)求k的值;
(2)設(shè)g(x)=log4![]() ,若函數(shù)f(x)與g(x)的圖象有且只有一個(gè)公共點(diǎn),求實(shí)數(shù)a的取值范圍.
,若函數(shù)f(x)與g(x)的圖象有且只有一個(gè)公共點(diǎn),求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為邊長(zhǎng)為2的菱形,
為邊長(zhǎng)為2的菱形,![]() ,
,![]() ,面
,面![]() 面
面![]() ,點(diǎn)
,點(diǎn)![]() 為棱
為棱![]() 的中點(diǎn).
的中點(diǎn).

(1)在棱![]() 上是否存在一點(diǎn)
上是否存在一點(diǎn)![]() ,使得
,使得![]() 面
面![]() ,并說(shuō)明理由;
,并說(shuō)明理由;
(2)當(dāng)二面角![]() 的余弦值為
的余弦值為![]() 時(shí),求直線
時(shí),求直線![]() 與平面
與平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】容器中有![]()
![]() 種粒子,若相同種類(lèi)的兩顆粒子發(fā)生碰撞,則變成一顆
種粒子,若相同種類(lèi)的兩顆粒子發(fā)生碰撞,則變成一顆![]() 粒子;不同種類(lèi)的兩顆粒子發(fā)生碰撞,會(huì)變成另外一種粒子. 例如,一顆
粒子;不同種類(lèi)的兩顆粒子發(fā)生碰撞,會(huì)變成另外一種粒子. 例如,一顆![]() 粒子和一顆
粒子和一顆![]() 粒子發(fā)生碰撞則變成一顆
粒子發(fā)生碰撞則變成一顆![]() 粒子.現(xiàn)有
粒子.現(xiàn)有![]() 粒子
粒子![]() 顆,
顆,![]() 粒子
粒子![]() 顆,
顆,![]() 粒子
粒子![]() 顆,如果經(jīng)過(guò)各種兩兩碰撞后,只剩
顆,如果經(jīng)過(guò)各種兩兩碰撞后,只剩![]() 顆粒子. 給出下列結(jié)論:
顆粒子. 給出下列結(jié)論:
① 最后一顆粒子可能是![]() 粒子
粒子
② 最后一顆粒子一定是![]() 粒子
粒子
③ 最后一顆粒子一定不是![]() 粒子
粒子
④ 以上都不正確
其中正確結(jié)論的序號(hào)是________.(寫(xiě)出所有正確結(jié)論的序號(hào))
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知定義在R上的函數(shù)f(x)=2x-![]() .
.
(1)若f(x)=![]() ,求x的值;
,求x的值;
(2)若2tf(2t)+mf(t)≥0對(duì)于t∈[1,2]恒成立,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】二次函數(shù)![]() 的圖象頂點(diǎn)為
的圖象頂點(diǎn)為![]() ,且圖象在
,且圖象在![]() 軸上截得的線段長(zhǎng)為8.
軸上截得的線段長(zhǎng)為8.
(1)求函數(shù)![]() 的解析式;
的解析式;
(2)令![]() .
.
(ⅰ)求函數(shù)![]() 在
在![]() 上的最小值;
上的最小值;
(ⅱ)若![]() 時(shí),不等式
時(shí),不等式![]() 恒成立,試求實(shí)數(shù)
恒成立,試求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com