（1）若
，
，求證：
；
（2）已知
,且
, 求證:
與
中至少有一個小于2.
【解析】第一問利用均值不等式，可知
第二問中，
證明：（1）
（2）
名校課堂系列答案科目：高中數學 來源： 題型：
查看答案和解析>>
科目：高中數學 來源： 題型：
（本題滿分12分）已知函數
（x>0）．（1）若b≥
，求證
≥（e是自然對數的底數）；（2）設F(x)=
+
（x≥1，a∈R），試問函數F(x)是否存在最小值？若存在，求出最小值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
（本題滿分12分）已知函數
（x>0）．（1）若b≥
，求證
≥（e是自然對數的底數）；（2）設F(x)=
+
（x≥1，a∈R），試問函數F(x)是否存在最小值？若存在，求出最小值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源：2012-2013學年云南師大附中高考適應性月考（七）理科數學試卷（解析版） 題型：解答題
已知函數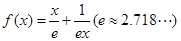
．
（1）若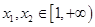
，
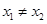，求證：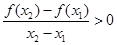
；
（2）若實數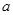
滿足
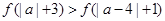．試求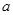的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
